Cuestiones de repaso

Explica las condiciones que debe tener un experimento para que siga una distribución binomial B(10, 0'5). Da un ejemplo de este experimento. ¿Cuánto vale la esperanza de esta distribución?

load (distrib) $
print (mean_binomial (10, 1/2)) ;  /* exacta */

sum (0:10 * dbinom (0:10, 10, 0.5)) # exacta
mean (rbinom (1e6, 10, 0.5))        # aproximada

[1] 5
[1] 5.002491

¿Cuánto vale la media de una variable aleatoria con distribución uniforme U(0, 4)?

/* exacta */
load (distrib) $
print (mean_continuous_uniform (0, 4)) ;

## aproximaciones
integrate (function (x) x * dunif(x,0,4), 0, 4) # determinista
mean (runif (1e6, 0, 4))                        # estocástica

2 with absolute error < 2.2e-14
[1] 2.000108

Sea X una variable que toma los valores {1, 2, 3, 4} con probabilidades {1/4, 1/8, 3/8, 1/4}. Calcula su función de distribución, su media y su varianza.

load (distrib) $
prob : [1/4, 1/8, 3/8, 1/4] $
F(x) := cdf_general_finite_discrete (x, prob) $
print ([mean_general_finite_discrete (prob),
         var_general_finite_discrete (prob)]) $

 21  79
[--, --] 
 8   64

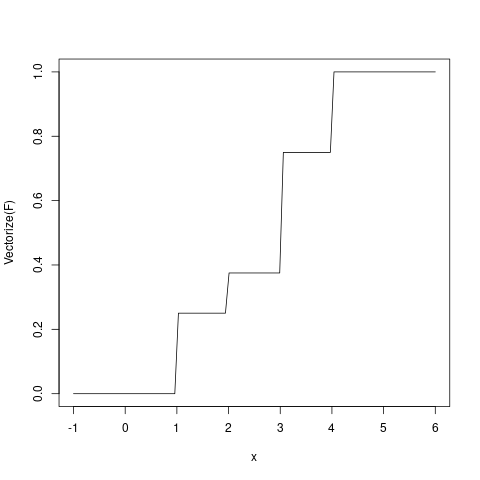
v <- 1:4
p <- c(1/4,1/8,3/8,1/4)
cat ("exactas\n")
F <- stepfun (v, c(0,cumsum(p)))
(media <- sum (v * p))
sum ((v-media)^2 * p) # varianza
F(2.5)                # ejemplo
cat ('aprox\n')
X <- sample (v, 1e6, TRUE, p)
F <- function (x) mean (X <= x)
mean (X)
var (X)
F(2.5)


exactas

[1] 2.625

[1] 1.234375

[1] 0.375

aprox

[1] 2.624319

[1] 1.23687

[1] 0.375373

plot (Vectorize(F), -1, 6)

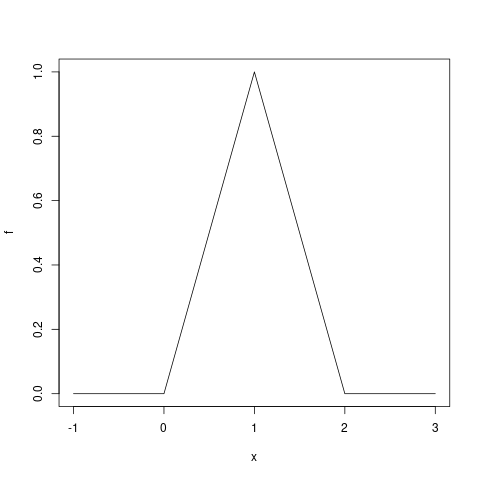
Sea \(X\) una variable con función de densidad \(f(x) =\)

\(x\) si \(0 < x < 1\)
\(2-x\) si \(1\le x < 2\)
\(0\) otramente

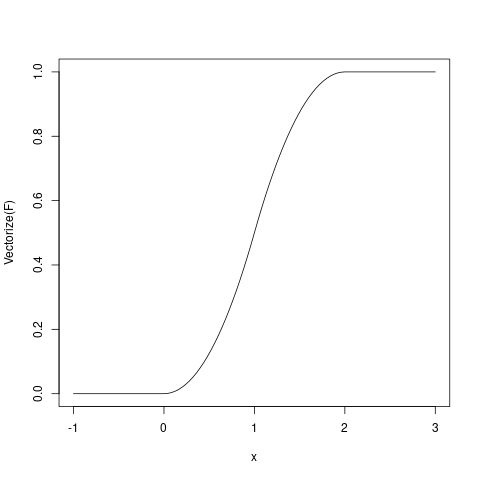
Calcula su función de distribución y represéntala gráficamente.

Calcula la media y la varianza de \(X\).

Calcula las probabilidades: \(\Pr (X \le 0.5)\) y \(\Pr (X > 1)\).

F(t) := if t<0 then 0
   else if t<=1 then integrate (x, x, 0, t)
   else if t<=2 then F(1) + integrate (2-x, x, 1, t)
   else 1 $

assume (0<y, y<1) $ print (F(y)) ;
assume (1<z, z<2) $ print (F(z)) ;

media : integrate (x * x,     x, 0, 1) + 
        integrate (x * (2-x), x, 1, 2) ;

varianza : integrate ((x-media)^2 * x,     x, 0, 1) + 
           integrate ((x-media)^2 * (2-x), x, 1, 2) ;

print (['media = media, 'varianza = varianza, 
        'F(0.5) = F(0.5), '(1-F(1)) = 1 - F(1)]) $

 2
y
-- 
2
    2
   z  - 4 z
(- --------) - 1 
      2
		       1           1             1
[media = 1, varianza = -, F(0.5) = -, 1 - F(1) = -] 
		       6           8             2

f <- function (x) ifelse (0<x & x<=1,
                          x,
                          ifelse (1<x & x<2,
                                  2-x,
                                  0))
F <- function (x) integrate (f, 0, x) $ value

(media <- integrate (function (x) x*f(x), 0, 2) $ value) # media
integrate (function (x) (x-media)^2*f(x), 0, 2)          # varianza

F(0.5)
1 - F(1)


[1] 1

0.1666667 with absolute error < 1.9e-15

[1] 0.125

[1] 0.5

plot (f, -1, 3)

plot (Vectorize(F), -1, 3)

## otra opción: install.packages("EnvStats")
f <- function (x) EnvStats::dtri(x, 0, 2, 1)
F <- function (x) EnvStats::ptri(x, 0, 2, 1)

¿Qué significa que la varianza de una variable sea 0?

\[ \text{Var} (X) = \text{E}[(X-\text E X) ^ 2] = \text {(discretas)} = \sum (x_i-\text E X) ^ 2 \Pr(X=x_i) \]
¿Qué mide la covarianza de dos variables X y Y?

\[ \text{Cov} (X,Y) = \text{E}[(X-\text E X) (Y-\text E Y)] = \text {(discretas)} = \sum (x_i-\text E X) (y_j-\text E Y) \Pr(X=x_i, Y=y_j) \]
- ¿A qué es igual la covarianza de una variable consigo misma?
- ¿Una covarianza igual a 40 es grande o pequeña?
- ¿Cómo se define y qué mide el coeficiente de correlación lineal de Pearson?
Para aproximar la probabilidad de que una pieza sea válida se revisan 50 piezas elegidas al azar, y se obtienen 48 válidas. Estima la probabilidad de que una pieza sea válida.
```
## X = "la pieza es válida" = B(p)
48 / 50 # estimación de p
```
```
[1] 0.96
```

¿Qué diferencia hay entre estimador y estimación? Utiliza el ejercicio anterior para dar un ejemplo de cada uno.

## estimador: la variable aleatoria que es función de la muestra
estimador.p <- function (X) mean (X == "válida")
muestra <- c (rep ("válida", 48), rep ("defectuosa", 2))
estimación.p <- estimador.p (muestra)

¿Cuál es la diferencia entre estadístico/estadígrafo y estimador? Da un ejemplo de estadígrafo que no sea estimador.

## Estrictamente, estimador es estadígrafo que toma valores
##  en el espacio paramétrico.
##  Entonces, si X = Exp(l), -sumaXi sería un estadígrafo que
##  toma valores negativos, luego no sería estimador.
## En el uso práctico, se denomina estimador al estadígrafo
##  definido con intención de que acerque al parámetro.
##  Así, n/sumaXi sería estimador de l, pero no sumaXi, 
##  aunque tome valores dentro del espacio paramétrico (0;inf)

¿Cómo se sabe si un estimador es “bueno”?
Sea \((X_1, ..., X_n)\) una muestra aleatoria simple de una variable \(X\) con media \(\mu\) y desvío típico \(\sigma\):
1. Calcula la esperanza y la varianza de la media muestral.
2. Calcula la esperanza de la varianza muestral.
Si \(X\) sigue una distribución beta \(\beta(4, 1)\), calcula la función de densidad y de distribución de la variable \(Y = -\ln(X)\), así como su esperanza y su varianza.
Reproductividad:
1. Sean \(X_1, \dots, X_m\) variables aleatorias independientes con distribución \(X_i \hookrightarrow B(n_i, p)\). ¿Cuál es la distribución de la suma \(X_1 + \dots + X_m\)?
2. Sean \(X_1, \dots, X_m\) variables aleatorias independientes con distribución \(X_i \hookrightarrow N (\mu_i, \sigma_i)\). ¿Cuál es la distribución de la suma \(X_1 + \dots + X_m\)? ¿Y la de la media?