Minería de datos

documento

documento

• cuenta.rda

• señales-eléctricas.*
• «medicion corriente.csv»

• usar objeto «ts»

  ?AirPassengers
  a <- AirPassengers
  a
  unclass (a)
  plot (a)
  start (a)
  end (a)
  frequency (a)
  plot (aggregate (a))              # totales anuales
  boxplot (a ~ cycle(a))            # medianas mensuales
  window (a, 1952, c(1953,12))      # datos de enero 1952 a diciembre 1953
  window (a, c(1952,1), c(1953,12)) # idem
  window (a, c(1952,8), freq=TRUE)  # datos de agosto
  

• generar objeto «ts»

  load ("temperaturas_one.rda") # portátil Acer Aspire One
  ls ()
  serie1 <- ts (temp1, freq=60) # periodo horario
  

EJERCICIO

• usar temperaturas_zadeh.rda
• crear serie temporal de «temp1.» con periodo horario, diario y semanal

install.packages ("xts")
library (xts)
ax <- as.xts (a)                      # AirPassengers
as.xts (b$Saldo, b$Fecha.Valor) -> bx # cuenta bancaria
## si dejamos «medicamento», se trasforma todo en cadenas:
tensionesx <- as.xts (tensiones[,-grep("fecha|medicamento",names(tensiones))], tensiones$fecha)
plot (tensionesx)
## el índice de tiempo puede tener formatos varios
class (index (ax))
as.Date (index (ax))
class (index (bx))
## se pueden extraer intervalos temporales usando fechas ISO: AAAA-MM-DD HH:MM:SS
ax["1953"]             # un año
ax["1953",]            # idem
ax["1953-10"]          # octubre
ax["/1953"]            # hasta cierto año
ax["1960-03/"]         # desde cierto mes
ax["1952-11/1953-03",] # entre fechas
first (ax, "2 year")   # primeros años
last  (ax, "3 month")  # últimos meses
## periodos
periodicity (ax)
periodicity (bx)
periodicity (tensionesx)
## extremos de los periodos
endpoints (tensionesx, "week")
endpoints (ax, "year")
## cambiar periodicidad
to.period (ax, "year")
plot (to.period (bx, "year"))
plot (to.period (tensionesx, "week"))
## describir por periodo
period.apply (tensionesx, endpoints(tensionesx,"month"), colMeans, na.rm=TRUE)

EJERCICIO

• Trasformar el dataframe datos de temperaturas_zadeh.rda en un objeto xts.
• Extrae los datos obtenidos hasta las 11h21 del 12 de diciembre de 2018.
• Obtén medias diarias, semanales y mensuales.

• serie \[\{x_t\mid t=1,\dots,n\}=\{x_1,\dots,x_n\}\]
• media \[\hat x = \frac{x_i}n \]
• predicción o pronóstico \[\hat x_{t+k\mid t}\]
• componentes
  • \(m_t\) tendencia
  • \(s_t\) estacionalidad
  • \(z_t\) residuo

• aditivo \[x_t = m_t +s_t +z_t\]
• multiplicativo \[x_t = m_t \cdot s_t +z_t\]

• tendencia
  • media móvil; p.ej. anual \[\hat m_t = \frac{\frac12 x_{t-6}+x_{t-5}+\dots+x_{t+5}+\frac12 x_{t+6}}{12}\]
  • regresión local (loes)
• estacionalidad
  • aditiva: \[\hat s_t = x_t - \hat m_t\]
  • multiplicativa: \[\hat s_t = \frac{x_t}{\hat m_t}\]

plot (decompose (a))                 # aditiva
plot (stl (a, "periodic"))           # idem mediante loes
plot (decompose (a, type="mult"))    # multiplicativa
decompose                            # usa «filter» para media móvil
identical (filter (a, c(1/2,rep(1,11),1/2)/12), decompose (a) $ trend)
saldo <- decompose (ts (to.period(bx,"month")$bx.Close, 
                        start = c(2003,11), 
                        freq  = 12))
plot (saldo)
saldo$figure   # efecto estacional (desde noviembre)

EJERCICIO

• Comenta la descomposición de la serie temperaturas_one con periodos de 60 (minutos).
• Prueba a descomponer algunas series de tensionesx semanales a partir de máximos diarios.
• Prueba a descomponer algunas series de temperaturas_zadeh con periodos diarios o semanales.

• ante todo, eliminar tendencia y estacionalidad
• la media puede cambiar, pero no hay información sobre el signo o magnitud del cambio
• ejemplo: ventas de un producto bien establecido en un mercado estable
• modelo \[\mu_t+w_t\]
  • \(\mu_t\) media no estacionaria
  • \(w_t\) desviaciones aleatorias independientes de media 0 y desviación típica \(\sigma\)
• estimación \[a_t = \alpha\,x_t+(1-\alpha)\,a_{t-1}\]
  • media móvil exponencialmente ponderada

    

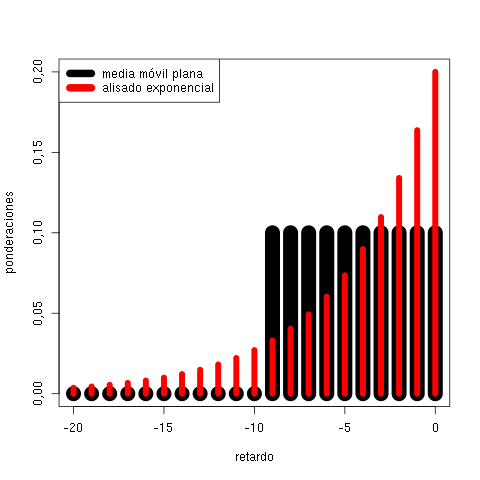
  • \(\alpha\) es el parámetro de alisado (habitualmente 0,2)
  • una estimación \(\hat\alpha\) puede obtenerse con R:

    library (xts)
    pulso.mat <- to.period (tensionesx$pulso.mat, "week") [,2]
    plot (pulso.mat) 
    ts.plot (pulso.mat) # permite añadir «lines» fácilmente
    lines (runmed(pulso.mat, 11), col=2, lwd=3)
    lines (filter(pulso.mat, rep(1/11,11)), col=3, lwd=3)
    lines (lowess(pulso.mat), col=4, lwd=3) # mismo alisado que «stl»
    lines (lowess(pulso.mat,f=1/3), col=5, lwd=3)
    plot (print (HoltWinters (pulso.mat, alpha=NULL, beta=FALSE, gamma=FALSE)))
    plot (print (HoltWinters (pulso.mat, alpha=0.1,  beta=FALSE, gamma=FALSE)))
    

  • método de Holt y Winters (aditivo; existe versión multiplicativa) \[a_t = \alpha\,(x_t-s_{t-p})+(1-\alpha)\,(a_{t-1}+b_{t-1})\] \[b_t = \beta\,(a_t-a_{t-1})+(1-\beta)\,b_{t-1}\] \[s_t = \gamma\,(x_t-a_t) + (1-\gamma)\,s_{t-p}\] donde
    • \(p\) es el periodo
    • \(a_t\) en el nivel (tendencia general)
    • \(b_t\) es la pendiente (trend en la ayuda de R de «HoltWinters») o cambio del nivel
    • \(s_t\) es el efecto estacional
    • la esperanza de \(x_t\) sería \(a_t + s_t\)
    • la predicción es \(\hat x_{n+k\mid n} = a_n + k\,b_n+s_{n+k-p}\) (\(k\leq p\))

    HW <- function (serie, umbral, alpha=NULL, beta=NULL, gamma=NULL, seasonal="additive")
    {
        ajustados <- window (serie, end=umbral)
        hw <- HoltWinters (ajustados, alpha=alpha, beta=beta, gamma=gamma,
                           seasonal=seasonal)
        pr <- predict (hw, floor((tsp(serie)[2]-umbral)*frequency(serie)))
        plot (serie)
        fi <- hw$fitted[,"xhat"]
        lines (as.vector(time(fi)), fi, col=3)
        lines (pr, col=2)
    }
    HW (AirPassengers, 1955, beta=FALSE, gamma=FALSE)
    HW (AirPassengers, 1955, gamma=FALSE)
    HW (AirPassengers, 1955, beta=FALSE)
    HW (AirPassengers, 1955)
    HW (AirPassengers, 1955, seasonal="multiplicative")
    

• valores independientes
• valores con media 0
• valores con la misma distribución estadística
• si se trata de N\((0;\sigma)\) entonces es ruido blanco gausiano

  plot (rnorm (100), type="l")
  

EJERCICIO

• representar histograma de ruido blanco
• representar correlograma de ruido blanco

• \(x_t\) es paseo aleatorio si \[x_t=x_{t-1}+w_t=\sum_{s=1}^t w_s\]

w <- rnorm (1000)
x <- cumsum (w)
plot (x, type="l")
acf (x)
acf (diff (x))

EJERCICIO

• estudiar las correlaciones de diferencias de las series de ejemplo

• AR(p) = modelo autorregresivo de orden \(p\) \[x_t=\alpha_1\,x_{t-1}+\dots+\alpha_p\,x_{t-p}+w_t\] donde \(w_t\) es ruido blanco
• paseo aleatorio = AR(1) con \(\alpha_1=1\)
• alisado exponencial = AR(p) con \(\alpha_i=\alpha\,(1-\alpha)^i\)
• estimación mediante regresión sobre retardos

## AR(1) con coeficiente positivo
x <- w <- rnorm (1000)
for (t in 2:1000) x[t] <- 0.9 * x[t-1] + w[t]
plot (x, type="l")
acf (x)
## AR(1) con coeficiente negativo
x <- w <- rnorm (1000)
for (t in 2:1000) x[t] <- -0.9 * x[t-1] + w[t]
plot (x, type="l")
acf (x)
## AR(2)
x <- w <- rnorm (1000)
for (t in 3:1000) x[t] <- x[t-1] -0.6 * x[t-2] + w[t]
plot (x, type="l")
acf (x)

• \(t\) tiempo
• \(\omega\) frecuencia (velocidad en radianes por unidad de tiempo)
• \(f\) frecuencia (velocidad en Hz = hercios = ciclos por unidad de tiempo) \(\omega=2\pi\,f\)
• en R, frecuencia en ciclos por intervalo de muestreo
• \(\frac{2\pi}{\omega}\) periodo (tiempo por ciclo)
• \(A\) amplitud
• \(\psi\) fase
• onda senoidal \[A\,\mbox{sen}(\omega\,t+\psi) = A\,\mbox{cos}(\psi)\,\mbox{sen}(\omega\,t)+ A\,\mbox{sen}(\psi)\,\mbox{cos}(\omega\,t)\]

• sea \(n\) par y sea la serie \(x_t\) con \(t=1,\dots,n\)
• \(n\) longitud de registro
• intervalo de muestreo = tiempo entre \(t\) y \(t+1\)
• considerar la regresión de \(x_t\) frente a \(n-1\) variables regresoras (serie de Fourier finita para una serie temporal discreta)
  • \(\mbox{cos}\left(\frac{2\pi\,t}{n}\right)\) => coeficiente \(a_1\)
  • \(\mbox{sen}\left(\frac{2\pi\,t}{n}\right)\) => coeficiente \(b_1\)
  • \(\mbox{cos}\left(\frac{4\pi\,t}{n}\right)\) => coeficiente \(a_2\)
  • \(\mbox{sen}\left(\frac{4\pi\,t}{n}\right)\) => coeficiente \(b_2\)
  • \(\mbox{cos}\left(\frac{6\pi\,t}{n}\right)\) => coeficiente \(a_3\)
  • \(\mbox{sen}\left(\frac{6\pi\,t}{n}\right)\) => coeficiente \(b_3\)
  • …
  • \(\mbox{cos}\left(\frac{2(n/2-1)\pi\,t}{n}\right)\) => coeficiente \(a_{n/2-1}\)
  • \(\mbox{sen}\left(\frac{2(n/2-1)\pi\,t}{n}\right)\) => coeficiente \(b_{n/2-1}\)
  • \(\mbox{cos}(\pi\,t)\) => coeficiente \(a_{n/2}\)

  \[x_t = a_0+a_1\,\mbox{cos}\left(\frac{2\pi\,t}{n}\right)+\dots+a_{n/2}\,\mbox{cos}(\pi\,t)\]

• número de coeficientes = longitud de serie => ajuste exacto (suele calcularse con algoritmo FFT)
  • \(a_0=\bar x\)
  • frecuencia más baja = 1 ciclo por longitud de registro = \(2\pi\) radianes por intervalo de muestreo
  • frecuencia más alta = 0,5 ciclos por intervalo de muestreo => de \(-1\) a \(+1\) en cada intervalo
• armónico
  • \(m\)-ésimo = senoidal que hace \(m\) ciclos en la longitud de registro
  • primer armónico = frecuencia fundamental
  • amplitud del armónico \(m\)-ésimo \[A_m=\sqrt{a_m^2+b_m^2}\]
• teorema de Parseval \[\frac1n = \sum_{t=1}^n x_t^2=A_0^2 + \frac12\sum_{m=1}^{(n/2)-1} A_m^2+A_{n/2}^2\] \[\mbox{Var}\,(x)=\frac12\sum_{m=1}^{(n/2)-1} A_m^2+A_{n/2}^2\]
  • se basa en que los términos de senos y cosenos están incorrelados
  • tabla de armónicos

    armónico	periodo	frecuencia \(f\)	frec. \(\omega\)	contribución a la varianza
    1	\(n\)	\(1/n\)	\(2\pi/n\)	\(\frac12A_1^2\)
    2	\(n/2\)	\(2/n\)	\(4\pi/n\)	\(\frac12A_2^2\)
    3	\(n/3\)	\(3/n\)	\(6\pi/n\)	\(\frac12A_3^2\)
    \(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
    \(n/2-1\)	\(n/(n/2-1)\)	\((n/2-1)/n\)	\((n-2)\pi/n\)	\(\frac12A_{n/2-1}^2\)
    \(n/2\)	2	\(1/2\)	\(\pi\)	\(A_{n/2}^2\)

• periodograma crudo o espectro de Fourier
  • diagrama de \(A_m^2\) frente a \(m\)
  • en R: spectrum (x)
  • intervalo de confianza asimétrico
• periodograma alisado o espectro muestral
  • en R: spectrum (x, span=k)
  • \(k\) en el número impar de muestras para la media móvil de Daniell
  • ponderaciones de Daniell = (1/2; 1; 1; …; 1; 1; 1/2) : (k-1)
  • mejor que ponderaciones constantes porque disminuye la influencia de la varianza de las frecuencias no-Fourier sobre el espectro de Fourier

• tratamiento de datos capturados
  • parámetros de la onda estimados por regresión no lineal
  • uso de trasformada de Fourier
  • cálculo de distorsión armónica total

  ## función para calcular armónicos, tasa de distorsión...
  estima <- function (x,                        # abscisas = tiempo
                      y,                        # ordenadas = señal
                      graf=TRUE,                # si representar gráficos
                      ## estimaciones iniciales de los parámetros:
                      m0=mean(y),               # altura del eje horizontal
                      a0=diff(range(y))/2,      # amplitud = (max-min):2
                      s=spectrum(y,plot=FALSE), # para calcular frecuencia
                      ## omega = intervalo de muestreo
                      omega0=s$freq[which.max(s$spec)]/diff(range(x))*length(x),
                      psi0=0)
  {
      p <- nls (y ~ m + a * sin (2*pi * omega * x + psi),
                start = list(m=m0, a=a0, omega=omega0, psi=psi0))
      if (graf) plot (x, y, type="l", xlab="microsegundos", ylab="") # original 
      if (graf) lines (x, predict (p, data.frame(x=x)), col=2)       # sinusoide ajustada
      periodo <- 1/coef(p)["omega"]
      psi     <- coef(p)["psi"]
      desplaz <- (2*pi*(psi>0) - psi) / (2*pi) * periodo
      if (coef(p)["a"] < 0) desplaz <- desplaz + periodo/2 # si amplitud negativa
      i  <- which (desplaz <= x & x < desplaz + periodo)   # índices de ciclo entero
      Y  <- fft (y[i])
      ai <- seq (1, 7, 2) # armónicos
      na <- length(ai)
      a  <- c (0, ai, length(Y) - ai)
      pa <- function (n) # predictora mediante armónicos
          Re (sum (Y[a+1] * exp (1i * 2*pi * a * n / length(Y)))) / length(Y)
      yt <- sapply (0:(length(x)-1) - sum(x<desplaz), pa)
      if (graf) lines (x, yt, type="l", col=3) # ajustada a partir de armónicos
      list (modelo = p,
            periodo = periodo,
            desplaz = desplaz,
            cc      = Y[1],
            armonic = Y[ai+1],
            distors = sqrt (sum (Mod (Y[ai[-1]+1]) ** 2)) / Mod(Y[ai[1]+1]),
            ajustad = yt,
            ruido   = y - yt)    
  }
  ## función auxiliar
  d.t.trun <- function (x, ...) # para desviación típica truncada con «trim»
      sqrt (mean ((x - mean (x, ...)) ^ 2, ...))
  ## función para presentar la información estimada
  informe <- function (x, y, ...)
  {
      e <- estima (x, y, ...)
      cat ("DISTORSIÓN =", e$distors, ".\n")
      ## límites para la detección de impulsos
      limites <- median (e$ruido) + 6 * c(-1,1) * d.t.trun (e$ruido, trim=0.05)
      cat ("IMPULSOS en los instantes:",
           x[e$ruido < limites[1] | e$ruido > limites[2]], ".\nFIN de IMPULSOS.\n")
  }
  

• ejemplo 1: ondas regulares (con eventuales impulsos)

  d <- read.csv2("señales-eléctricas.csv") # cargamos datos
  x <- d[,1]                               # tiempo
  for (s in 2:5) {
      y <- d[,s]                           # señal (2, 3, 4, 5)
      cat (paste ("COLUMNA",s,"\n"))
      informe (x, y)
  }
  

• ejemplo 2

  ## - Valores entre 0 y 1023 (extremos de la escala de medida).
  ## - El valor 512 corresponde al valor nulo.
  ## - La corriente máxima a la que corresponde la señal es 0,7 A
  ## - La potencia aproximada es Imax/sqr(2).230.
  y <- scan("medicion corriente.csv")
  x <- 1:length(y)
  informe (x, y)
  ## intentamos de nuevo con una parte regular
  X <- x[1:500]
  Y <- y[1:500]
  informe (X, Y)
  ## estimación de la amplitud
  e <- estima(X,Y)
  amplitud <- diff(range(e$ajustad))/2
  cat ("AMPLITUD = ", amplitud, "\n")
  ## buscamos zona con anomalía
  yt <- predict(e$modelo,data.frame(x=x))
  diferencias <- abs (y - predict(e$modelo,data.frame(x=x)))
  anomalo.desde <- x [which (diferencias/amplitud > 0.3) [1]]
  plot(x,y,type="l"); lines(x,yt,col=3); abline(v=anomalo.desde,col=2)
  

• sea la serie \[x_t = \theta(t)+\epsilon_t\]
• se puede sospechar que existe \(\tau\) tal que
  • cambio de media: \[x_t=\theta_0(t)+\epsilon_t\qquad t=1,\dots,\tau-1\] \[x_t=\theta_1(t)+\epsilon_t\qquad t=\tau,\dots,T\phantom{-1}\] consideraremos el caso \(\theta_0\) y \(\theta_1\) y Var\((\epsilon_t)=\sigma^2\) constantes
  • cambio de varianza \[\mbox{Var}(\epsilon_t)=\sigma_0^2\qquad t=1,\dots,\tau-1\] \[\mbox{Var}(\epsilon_t)=\sigma_1^2\qquad t=\tau,\dots,T\phantom{-1}\]
• \(\tau\) sería un punto de cambio

• distribución estadística de la característica observada
  • atributo dicótomo
    • B(1;p)
  • variable cuantitativa
    • N(mu;sigma)
    • desconocida con media mu y desviación sigma
• parámetro de interés
  • p
  • mu
  • sigma
• muestra de control
  • n = tamaño muestral
  • ¿independencia entre observaciones?
    • ¿representa la muestra la variabilidad esperada bajo control?
• nivel de significación
  • H0: parámetro = valor de referencia
  • H1: parámetro ≠ valor de referencia
  • 3 sigma => nivel de significación bilateral 0,0027

• paquete «changepoint» para detectar cambios
  • en medias: cpt.mean
  • en varianzas: cpt.var
  • en ambas: cpt.meanvar
• algoritmos
  • un solo cambio
    • AMOC (usado por omisión) Hinkley 1970
  • varios
    • PELT Killick 2012
    • SegNeigh Auger 1989
    • BinSeg Scott 1974
• penalizaciones
  • verosimilitud penalizada
    • revisión de Killick
    • \( 2\,\log\,\max\,L - p\,\phi(n) \)
    • \(p\) es el número de parámetros, incluidos los puntos de cambio
    • \(n\) es el tamaño muestral
  • "None"
    • \(\phi(n) = 0\)
    • contraste de razón de verosimilitudes
    • el resto de métodos se usan fundamentalmente por poder ser generalizables a más de un punto de cambio
  • "AIC"
    • criterio de Akaike
    • \(\phi(n) = 2\)
    • asintóticamente sobrestima el número de parámetros
  • "SCI"
    • criterio de Schwarz
    • \(\phi(n) = \log\,n\)
  • "Hannan-Quinn"
    • criterio de Hannan y Quinn
    • \(\phi(n) = \log\,\log\,n\)
  • "BIC", "MBIC"
    • métodos bayesianos
    • dependen de probabilidades a priori

library (changepoint)
x <- c (rnorm(150,0,1), rnorm(50,0.5,1))  # tau = 151
## alisado para apreciar cambios
plot (x, type="l"); lines (runmed (x, 51),           col=2, lwd=5)
plot (x, type="l"); lines (filter (x, rep(1,51)/51), col=2, lwd=5)
plot (x, type="l"); lines (lowess (time(x), x),      col=2, lwd=5)
library (changepoint)
puntos <- cpt.mean (x)
puntos                                    # puede detectar 0 ó 1
plot (puntos)
example (cpt.mean)                        # varios puntos de cambio de media
example (cpt.var)                         # de varianza
example (cpt.meanvar)                     # de media y varianza

EJERCICIO

• Comparar la efectividad de la penalización por omisión ("MBIC") con la de «penalty="None"» (u otras) en le ejemplo «x <- c (rnorm(150,0,1), rnorm(50,0.5,1))».
• Halla la potencia de detección de un cambio el función del salto de la media (\(\alpha\)): «x <- c (rnorm(150,0,1), rnorm(50,\(\alpha\),1))».
• Ídem pero suponiendo un modelo autoregresivo \(x_t = \mu_{0/1}+0.9\,x_{t-1}+w_t\).
• Prueba diferentes métodos para detectar cambios en los datos de ejemplo (tensiones, temperaturas…).