Introducción a R
Índice
- 1. Historia
- 2. Instalación
- 3. Estadística básica con Rcmdr
- 4. Lenguaje: elementos básicos
- 5. Estadística básica programando
- 6. Lenguaje: avanzado
1 Historia
1.1 Python
- en GNU/Linux se extendió el uso del lenguaje a alto nivel Perl para todo tipo de tareas:
- administración del sistema
- programación web
- análisis de datos
- …
- Python fue sustituyendo a Perl porque
- es mucho más legible
- la sintaxis de Perl usa muchos combinaciones de símbolos extrañas
- Python se estructura según sangría y parece seudocódigo
- facilita reúso del código fuente
- lema de Perl: hay más de una manera de hacerlo
- lema de Python: debería haber sólo una manera obvia de hacerlo
- es mucho más legible
- lenguaje de programación a alto nivel de propósito general
- como Perl, Ruby, Lisp…
- muchas bibliotecas: pilas incluidas
1.2 R
- lenguaje de programación de propósito matemático
- como Octave/Matlab, Maxima…
- originalmente se diseñó el lenguaje
Spara estadística- su nombre está inspirado por el del lenguage
Cy por la palabra statistics
- su nombre está inspirado por el del lenguage
R
2 Instalación
2.1 Python
2.1.1 Windows
- Descargar el instalador de https://www.python.org/downloads/windows, por ejemplo, Latest Python 3 Release
Una vez instalado, ejecutar en el terminal
cmd.exe(quizá haya que pulsar intro alguna vez):py -m pip install --user --upgrade pip py -m pip install --user numpy scipy pandas statsmodels matplotlib sklearn
- Otra posibilidad es usar conda
- sistema de paquetería basado en Python
- ventajas:
- multiplataforma
- facilita distribución de programas (p.ej. qiime2)
- no requiere privilegios de administrador
- inconveniente: duplica muchas bibliotecas instaladas por la paquetería del sistema operativo
2.1.2 Debian
apt install python3-pandas python3-dill python3-sklearn # módulos necesarios para tratar datos apt install python-numpy-doc python-scipy-doc python-pandas-doc python-sklearn-doc # documentación
Conviene instalar algún editor, por ejemplo,
apt install idle-python3.8 apt install spyder apt install emacs apt install jupyter jupyter-notebook python3-ipykernel
2.2 R
2.2.1 Windows
- Descargar el último R desde https://cran.r-project.org/bin/windows/base
- Recomendaciones si se va a usar
Rcmdr- Tras ejecutar el fichero
.exedescargado, pulsar Siguiente hasta el diálogo Opciones de configuración. Ahí elegir Sí y pulsar Siguiente. - Elegir en Modo de display la opción SDI - ventanas separadas.
- Mantener las opciones por omisión en el resto de diálogos, hasta Instalando.
- Al pinchar en el icono se abre el programa R Gui.
- Tras ejecutar el fichero
- Interfases opcionales:
Para facilitar el uso básico y el aprendizaje: el paquete
Rcmdr(commander); instalarlo desde el menúPaquetesdelRGuio escribiendo en laR Consolela siguiente orden:install.packages ("Rcmdr")Ejecutar en la consola de R la orden
library(Rcmdr)
- Cuando pregunte si instalar paquetes adicionales, pulsar Sí.
- Es posible que pregunte en algún momento si instalar paquetes en un directorio alternativo. Aceptar el que da por omisión.
- El entorno más popular: RStudio
- Emacs Speaks Statistics desde Emacs para Windows
2.2.2 Debian
2.2.2.1 instalar R
todos los paquetes (ocupa varios gigas)
apt install r-*
sólo lo más básico
apt install r-base
los paquetes más habituales
apt install r-recommended
Ojo a la diferencia entre paquetes APT (de Debian, programas
empaquetados para ser fácilmente instalables en Debian) y paquetes
de R (bibliotecas o extensiones de R). Hay paquetes de R (por
ejemplo, Rcmdr) que tienen su propio paquete de Debian (siguiendo
el ejemplo, r-cran-rcmdr), pero otros muchos no.
Si necesitas un paquete de R más específico, es normal que no sea compatible con la versión de R instalada de fábrica en Debian/Ubuntu (sobre todo, si estás usando Debian Stable o Ubuntu LST, long time support). En ese caso, hay que añadir un repositorio al APT. Los detalles están en https://cran.r-project.org/bin/linux/
2.2.2.2 uso desde terminal
$ cd ~/directorio/de/trabajo $ R > q() # para salir Save workspace image? [y/n/c]: n
Si se pulsa y para salir, entonces aparecen los ficheros .Rhistory y .RData. El primero contiene los comandos
ejecutados en la sesión y el segundo alberga los objetos creados. Ejemplo:
$ R > variable = "texto de ejemplo" > q() Save workspace image? [y/n/c]: y $ R > variable # comprobamos que el valor se había guardado
Si pulsamos la flecha hacia arriba (ó Ctrl-P) entonces recuperamos los comandos de la sesión anterior.
Esto es útil si arrancamos R en directorios distintos para sesiones de trabajo que tengan que ver con cosas distintas.
Para editar un programa de R dentro de la sesión, puede usarse:
$ R
> system ("gedit miprograma.R&") # el símbolo & implica ejecución en segundo plano (asíncrona)
2.2.2.3 instalar interfases opcionales
2.2.2.3.1 Rcmdr
Se puede instalar como paquete de APT así
apt install r-cran-rcmdr
Se podría instalar desde dentro de R así:
install.packages("Rcmdr")
Puede aparecer como icono en el lanzador de aplicaciones, o se puede arrancar desde R con la orden
library(Rcmdr)
Si ya se ha ejecutado esa orden y, habiendo salido de Rcmdr, se quiere volver a entrar sin salir de R, ejecútese
Commander()
Si has usado Rcmdr desde terminal, al salir de Rcmdr puede haberse corrompido el terminal.
Escribiendo reset e intro se vuelve a la normalidad.
2.2.2.3.2 Rkward
apt install rkward
- Tiene un buen editor de datos en forma de cuadrícula o rejilla de hoja de cálculo.
- En los menús sólo implementa recodificación de variables cualitativas. Las trasformaciones más complejas deben hacerse desde la consola.
- A medio camino entre Rcmdr y Rstudio.
2.2.2.3.3 Emacs speaks statistics
apt install ess
Probablemente el mejor entorno integrado para programar en R, sobre todo si prefieres moverte con el teclado en vez de con el ratón.
Emacs también es un buen entorno para programar en Python, Octave, Maxima, \(\LaTeX\), etc.
2.2.2.3.4 Rstudio
Se puede usar Rstudio en Debian, aunque no está integrado en un repositorio APT, lo que dificulta la instalación. Los pasos serían:
Descargar el fichero http://rstudio.com -> Download -> RStudio Desktop -> All-installers -> Ubuntu 18 / Debian 10 -> rstudio-2021.09.2-382-amd64.deb
Se puede comprobar la integridad del fichero usando el comando
sha256sum.Instalarlo desde un terminal:
dpkg -i ruta/al/fichero/rstudio-2021.09.2-382-amd64.deb
Si diese error por faltar algún paquete, se han de instalar los paquetes faltantes con una orden similar a ésta:
apt install libedit2 libssl1.1 libclang-dev libxkbcommon-x11-0 libsqlite3-0 libpq5 libc6
La lista necesaria puede obtenerse así:
dpkg -I rstudio-2021.09.2-382-amd64.deb | grep Depend
2.2.2.3.5 jupyteR
instalar (como "root" o tecleando antes "sudo"):
apt install jupyter r-cran-irkernel jupyter-notebook jupyter-nbconvert
arrancar el navegador con la sesión interactiva:
jupyter notebook
pulsar New y luego R
- puede dar problemas (como no aparecer R en el menú New) si
el paquete de R llamado
base64encfue instalado antes de la versión 4; en tal caso, ejecutar en Rinstall.packages("base64enc")resuelve el problema
el R instalado en el sistema no es el correspondiente a la versión distribuida con el sistema operativo (p.ej. si se instala R desde CRAN); en tal caso, ejecútese en R:
install.packages("IRkernel") IRkernel::installspec()
para convertir una sesión a un formato estático como HTML, LaTeX…
jupyter nbconvert --to html miSesión.ipynb
3 Estadística básica con Rcmdr
3.1 instalación y carga del paquete Rcmdr
Si no se ha instalado previamente (por ejemplo mediante el sistema de paquetería del sistema operativo) puede instalarse ahora como paquete de R:
install.packages ("Rcmdr")
Para abrir el R-Commander:
library ("Rcmdr") # o bien: library(Rcmdr)
Si se cierra el Rcmdr sin salir de R, para volver a abrirlo hay que ejecutar
Commander()
Partes de la ventana de Rcmdr:
- barra de menús
- barra de elementos activos
- área de instrucciones - R Script - R Markdown
- área de salida
- área de mensajes
3.2 Obtener datos
3.2.1 De ejemplo
- Menú Datos, submenú Conjunto de datos en paquetes.
- Eligiendo alguno de los paquetes (datasets, carData…) se listan los conjuntos de datos disponibles.
- Los datos del paquete
datasets(por ejemplo,mtcars) están disponibles al arrancarRpero, al cargarRcmdr, se ocultan (para no abarrotar la lista de datos disponibles en la barra de elementos activos) y es necesario cargarlos explícitamente. - Ejercicio
- Cargar
mtcarsdel paquetedatasets. - Cargar
Chiledel paquetecarData.
- Cargar
3.2.2 En formato nativo de R
- Menú Datos, opción Cargar conjunto de datos.
- Habitualmente, dichos ficheros tienen extensión
.rdaó.RData. - Pueden contener
- un solo conjunto de datos (cuyo nombre puede coincidir o no con el nombre del fichero)
- múltiples conjuntos de datos, además de variables, funciones, etc. (entorno de trabajo de R)
- Ejercicio
- Cargar mtcoches.rda y comprobar la lista de datos disponibles
- Cargar iris.RData y comprobar la lista de datos disponibles
3.2.3 En formatos ajenos
- Menú Datos, submenú Importar datos.
- De especial interés es la importación de datos de texto (CSV)
- un renglón = un registro
- campos delimitados por un carácter
- csv = coma «,»
- csv2 = punto y coma «;»
- delim = tabulador
- table = espacio en blanco (espacios a tabuladores; uno o varios)
- codificación: utf-8 (unicode) o latin-1 (iso-8859-1)
- Ejercicio: intenta importar los siguientes conjuntos de datos
3.3 Guardar datos
- Menú Fichero, submenú Guardar el entorno de trabajo R como….
- Guarda todas las variables, incluyendo funciones y conjuntos de datos.
- Menú Datos, submenú Conjunto de datos activo, opción Guardar el conjunto de datos activo.
- Lo guarda con el formato nativo de R,
.rdaó.RData.
- Lo guarda con el formato nativo de R,
- Menú Datos, submenú Conjunto de datos activo, opción Exportar el conjunto de datos activo.
- Lo guarda en formato de tabla: registros separados por salto de renglón; campos separados por coma o punto-y-coma o tabulador… (llamado habitualmente CSV)
- Ejercicio:
- Guardar el entorno de trabajo de R como
cursoR.rda. Salir de R (sin salvar el entorno cuando pregunte), volver a entrar en R, cargar dicho fichero y comprobar que se conservan todos los datos. - Cargar el conjunto de datos de ejemplo llamado
mtcars. Exportarlo a un ficheromtcars.rday a un ficheromtcars.csv.
- Guardar el entorno de trabajo de R como
3.4 Descriptivos
- Menú Estadísticos, submenú Resúmenes, opción Conjunto de datos activo.
- Ídem, opción Distribución de frecuencias.
- Ídem, opción Resúmenes numéricos.
- Menú Gráficas, opciones
- gráfica de barras
- gráfica de sectores
- histograma
- diagrama de caja
- Ejercicio:
- Realizar un informe descriptivo univariante de
mtcars.
- Realizar un informe descriptivo univariante de
3.5 Modificar datos
- Menú Datos: Modificar variables…: Calcular…
- Menú Datos: Modificar variables…: Recodificar…
- Menú Datos: Modificar variables…: Reordenar niveles…
- Filtrar
- Ejercicio:
- Convertir al sistema métrico las siguientes variables de
mtcars: wt, disp, hp, mpg - Cargar los datos de ejemplo
Chiley crear un conjunto de datos llamadoChile.fque contenga los registros tales quesexseaFy tales queagesea menor que 50. - Hacer un diagrama de barras de la variable
educationcon el orden correcto.
- Convertir al sistema métrico las siguientes variables de
3.6 Distribuciones de probabilidad
- Menú Distribuciones
- Ejercicio:
- Generar un conjunto de cien valores aleatorios de la variable
alturacomo valores gausianos de media 170 y desvío típico 10. - Generar un conjunto de mil registros aleatorios que contenga la variable
trabajacon valoressí(probabilidad 30%) yno(probabilidad 70%).
- Generar un conjunto de cien valores aleatorios de la variable
3.7 Contrastes de hipótesis sobre medias, proporciones…
- Menú Estadísticos: Resúmenes: Test de normalidad.
- Menú Estadísticos: Medias: Test t para una muestra.
- Menú Estadísticos: Proporciones: Test de proporciones para una muestra.
- Menú Estadísticos: Test no paramétricos: Test de Wilcoxon para una muestra
- Menú Estadísticos: Proporciones: Test de proporciones para dos muestras.
- Menú Estadísticos: Varianzas: Test F para dos varianzas.
- Menú Estadísticos: Medias: Test t para muestras independientes.
- Menú Estadísticos: Medias: Test t para muestras relacionadas.
- Menú Estadísticos: Test no paramétricos: Test de Wilcoxon para dos muestras
- Menú Estadísticos: Test no paramétricos: Test de Wilcoxon para muestras pareadas
- Ejercicio:
- ¿Existen diferencias significativas entre los «consumos» (
mpg) de los coches demtcarscon distintasam? - La proporción de coches con cambio automático
entre los
vs=V¿es mayor que entre losvs=S?
- ¿Existen diferencias significativas entre los «consumos» (
3.9 Regresión lineal
- Estadísticos: Resúmenes: Matriz de correlaciones
- Gráficas: Matriz de diagrama de dispersión
- Gráficas: Diagrama de dispersión
- Estadísticos: Ajuste de modelos: Regresión lineal
- Modelos: Gráficos: Gráficas básicas de diagnóstico
- Ejercicio:
- Proponer un modelo para predecir el «consumo» a partir del resto de
variables de
mtcars.
- Proponer un modelo para predecir el «consumo» a partir del resto de
variables de
4 Lenguaje: elementos básicos
4.1 ayuda
4.1.1 R
Para encontrar ayuda sobre un comando de R, por ejemplo rep, puedes usar
?rep
Para algunos comandos con nombres especiales, hay que usar comillas; por ejemplo,
?"[" ?"if"
Si sólo conocemos parte del nombre del comando (p.ej. norm), usamos
apropos("norm")
Si queremos encontrar información relacionada con un concepto, podemos usar:
??variance
help.search("variance")
- https://cran.r-project.org/doc/contrib/R-intro-1.1.0-espanol.1.pdf
- «Spanish» en https://cran.r-project.org/other-docs.html
- tutoriales sobre técnicas variadas: quick R
- paquetes agrupados por campos: https://cran.r-project.org/web/views/
- gráficos: R graph gallery
4.1.2 Python
help("regression")
help("modules regression")
4.2 tipos de datos del lenguaje
4.2.1 simples
4.2.1.1 especiales
4.2.1.1.1 R
NULL- valor nulo; se produce cuando no hay otro resultado
NAnot available- se usa en ficheros de datos para indicar que el dato correspondiente está ausente
se produce como resultado de operaciones sin sentido, como al intentar trasformar
8798aue98en un númeroas.numeric("8798aue98")
NaNnot a numberse produce como resultado de algunas operaciones matemáticas
sqrt (-1) # raíz cuadrada log (-1) # logaritmo
4.2.1.1.2 Python
Noneimport numpy as np; np.nan>>> import math >>> math.log(np.nan) nan
4.2.1.2 lógicos (booleanos)
4.2.1.2.1 R
TRUE y FALSE
resultan de realizar comparaciones
10 < 15 # TRUE 10 > 15 # FALSE 3 == 3 # == igual 3 != 3 # != distinto identical(3,3) # se usa en vez de == cuando se comparan objetos compuestos
el operador unario «!» sirve para negar
!TRUE # da FALSE !FALSE # da TRUE
- operadores binarios
los operadores binarios «&» y «|» son, respectivamente, la conjunción copulativa («y» lógico) y la disyunción inclusiva («o» lógica)
TRUE & TRUE # da TRUE TRUE & FALSE # da FALSE FALSE & TRUE # da FALSE FALSE & FALSE # da FALSE TRUE | TRUE # da TRUE TRUE | FALSE # da TRUE FALSE | TRUE # da TRUE FALSE | FALSE # da FALSE
- existes dos versiones
de circuito largo (funcionan vectorialmente): «&» «|» (y, o)
TRUE & FALSE; TRUE | !FALSE c(TRUE,FALSE) & c(FALSE,TRUE) FALSE & sqrt(-1) # produce aviso porque se evalúan ambos operandos TRUE & sqrt(-1) # ídem
de circuito corto (resultado escalar): «&&», «||»
FALSE && sqrt(-1) # no produce aviso TRUE || sqrt(-1) # tampoco
suelen usarse en estructuras de control como
ifowhile
al comenzar la sesión, la variable
TvaleTRUEy laFvaleFALSE, lo que puede resultar cómodo para uso interactivoc(T,T,T,T,F,F,F,T,F,T)
se recomienda usar las palabras completas
TRUEyFALSEpara evitar problemas si se redefinenTóF
4.2.1.2.2 Python
True y False
operadores de circuito largo (no funcionan vectorialmente): «&» «|» (y, o, no)
import math as m False & m.sqrt(-1) # da error
operadores de circuito corto: «and» «or»
False and m.sqrt(-1) # sin error
- se pueden usar «&» «|» «~» (y, o, no) a la manera vectorial mediante
pandas
4.2.1.3 numéricos
4.2.1.3.1 R
- enteros:
58o bien58L - coma/punto deslizante (float):
102.23 - notación exponencial:
1e-6 - complejos:
5+3i(compararsqrt(-1)ysqrt(-1+0i))
4.2.1.3.2 Python
- enteros:
58o bien58L - coma deslizante:
102.23 - notación exponencial:
1e-6 - complejos:
5+3j(compararmath.sqrt(-1)ycmath.sqrt(-1))
4.2.1.4 caracteres
4.2.1.4.1 R
"cadena de texto"'cadena de texto'las dos formas anteriores son equivalentes; si se quiere incluir una comilla o un apóstrofo en la cadena, se debe usar el delimitador apropiado (el otro) o «escapar» el carácter mediante una retrobarra «\»:
'me dijo "gracias, tío"' "me dijo \"gracias, tío\"" "ye'l mio güelu" 'ye\'l mio güelu'
para extraer una subcadena: substring (cadena, posición primero, posición último)
substring ("cadena", 2, 4) # "ade" substring ("cadena", 1, 3) # "cad" substring ("cadena", 5, 5) # "n" substring ("cadena", 2) # "adena"
si se omite "posición último" se extrae hasta el final
(existe también "substr" pero no permite omitir el tercer argumento)
para tratar caracteres como números, puede hacer falta retocar la cadena:
as.numeric ("2.71") as.numeric (gsub (",", ".", "3,14"))
ojo, porque el primer argumento de 'gsub' es una expresión regular; por ejemplo, esto no funciona bien:
gsub (".", ",", "3.14")
hay que refinar la instrucción de alguna de estas maneras:
gsub ("\\.", ",", "3.14") # se utiliza «\» para «escapar» el punto en la expresión regular; ## a su vez, la retrobarra está escapada «\\» porque también es un carácter especial en R; gsub (".", ",", "3.14", fixed=TRUE) # interpreta la cadena como tal, no como expresión regular
4.2.1.4.2 Python
"cadena de texto"'cadena de texto'las dos formas anteriores son equivalentes; si se quiere incluir una comilla o un apóstrofo en la cadena, se debe usar el delimitador apropiado (el otro) o «escapar» el carácter mediante una retrobarra «\»:
'me dijo "gracias, tío"' "me dijo \"gracias, tío\"" "ye'l mio güelu" 'ye\'l mio güelu'
para extraer parte de una cadena se usan lonchas (slicing)
>>> "cadena"[2:5] 'den' >>> "cadena"[2:] 'dena' >>> "cadena"[:2] 'ca'
para tratar caracteres como números, puede hacer falta retocar la cadena:
float ("2.71") import re; float (re.sub (",", ".", "3,14"))
ojo con los caracteres especiales:
re.sub (".",",","3.14") re.sub ("\.",",","3.14")
4.2.2 compuestos
4.2.2.1 vectores
4.2.2.1.1 R
- creación
c(10,15,-3)10:30seq(-4,4,.1)c("uno","dos","tres")v <- 10:40 # asignación a variable; podría escribirse también así: v = 10:40
- selección de elementos mediante índices (números enteros)
v[10]v[-10]v[2:4] # del segundo al cuarto elementosv[c(1,2,4)]v[-c(1,2,4)]
- selección mediante booleanos:
v <- seq (10, 100, 10)v[8] <- NA(para ver la diferencia al usarwhichysubset)v > 55v[v>55]v[which(v>55)]subset(v,v>55)l <- letters[1:10]l[v>55]; l[which(v>55)]
- todos los escalares son vectores de longitud 1
los vectores son homogéneos; los elementos promocionan al tipo más general:
c (0, 1, 2, TRUE, FALSE) # produce 0 1 2 1 0 c( 0, 1, TRUE, FALSE, "hola") # produce "0" "1" "TRUE" "FALSE" "hola"
- vectores como conjuntos (sean
v1 <- c(2, 4, 6), v2 <- 1:3)pertenencia
1 %in% v1; v2 %in% v1
unión
union (v1, v2)
intersección
intersect (v1, v2)
diferencia
setdiff (v1, v2)
vectores con nombres
> v <- c(alfa=3,beta=88,gama=-5) > v alfa beta gama 3 88 -5 > names (v) [1] "alfa" "beta" "gama" > names (v) <- c("A","B","C") > v A B C 3 88 -5 > v["B"] B 88 > w <- c(primero=TRUE,segundo=FALSE) > w primero segundo TRUE FALSE > as.numeric(w) # pierde nombres [1] 1 0 > +w # forma más rápida de mantenerlos: https://stackoverflow.com/questions/37951199 primero segundo 1 0 > u <- c(uno=1,dos=2,tres=3,cuatro=4,cinco=5) > u[-c(2,3)] uno cuatro cinco 1 4 5 > u[-c("dos","tres")] # no funciona Error in -c("dos", "tres") : argumento no válido para un operador unitario > u[setdiff(names(u),c("dos","tres"))] uno cuatro cinco 1 4 5 > u [! names(u) %in% c("dos","tres")] uno cuatro cinco 1 4 5
ejemplos
(t <- table(mtcars$am)) # paréntesis para mostrar resultado de asignación 100 * t / sum(t) # porcentajes conservan etiquetas quantile (mtcars$hp, c(1/2,3/4)) # con etiquetas quantile (mtcars$hp, c(1/2,3/4), names=FALSE) ## para evitar asignar nombres a posteriori: num <- 1:9 setNames(sqrt(num),paste("raíz de",num))
4.2.2.1.2 Python
El tipo básico más similar sería la lista, que es heterogénea:
[10, 15, -3, "hola"]
Pueden crearse vectores homogéneos como en R recurriendo al módulo numpy:
from numpy import arraya = array ([10, 15, -3]) # de enterosa = array ([10, 15, -3.0]) # de reales3 * a # permiten operaciones elemento a elemento
Los rangos deben convertirse explícitamente:
list(range(10,31)) # desde 10 hasta 30from numpy import arange; list(arange(-4.0,4.0,.1)) # hasta 3,9["uno", "dos", "tres"]v = range(10,40) # del 10 al 39v[0] # el primer elementov[29] # el últimov[-1] # el último elementov[1:4] # del segundo al cuarto elementos[v[i] for i in 0,1,3][v[i] for i in range(0,30) if not(i in [0,1,3])]- selección mediante booleanos:
v = arange (10.0, 101, 10)(nanno es entero, sino real)from numpy import nan; v[8] = nanv > 55(elnanproduceFalse)v[v>55]
- los escalares no son listas de longitud 1:
3+4; [3]+[4](comparar conarray([3])+array([4]) la asignación de listas o arrayes en Python crea referencias, punteros; no como en R, que crea copias:
R> x = c(5,6); y = x; y[1] = 10; x # produce: 5 6 python>>> x = [5,6]; y = x; y[0] = 10; x # produce: 10 6
Para los conjuntos se usan llaves en vez de corchetes:
w1 = set ([1, 2, 3])w2 = {2, 4, 6}pertenencia
1 in w1
unión
w1.union(w2)
intersección
w1.intersection(w2)
diferencia
w1.difference(w2)
Para usar etiquetas para los elementos, recurriremos a diccionarios de Python básico o a Series de Python-Pandas:
v = {"alfa": 3, "beta": 88, "gama": -5}
v.keys()
import pandas as pd, numpy as np
s = pd.Series([1,3,5,np.nan,6,8])
s = pd.Series ([1,3,5,np.nan,6,8], index=["uno","dos","tres","cuatro","cinco","seis"])
s.keys()
w = pd.Series (v)
4.2.2.2 matrices
4.2.2.2.1 R
m <- matrix (1:9, 3)- crear una matriz a partir de un vector
- se indica el número de filas (
3) - para indicar el de columnas:
matrix (..., ncol = 3) - la matriz se rellena por columnas
- para rellenarla por filas:
matrix (..., byrow = TRUE)
- submatriz:
m[1:2,2:3] - vector con primera fila:
m[1,] - vector con primera columna:
m[,1] - si se quiere mantener como matriz columna:
m[,1,drop=FALSE] - asignación:
- a un elemento:
m[2,3] <- 11 - a una submatriz:
m[1:2,2:3] <- 100
- a un elemento:
- traspuesta:
t(m) - determinante:
det(m) - inversa:
solve(m) - producto matricial:
m%*%m cbind (m, m); rbind (m, m)cbind= pegar varias matrices al ladorbind= pegar varias matrices de arriba a abajo
como los vectores, las matrices son homogéneas: todos sus elementos son del mismo tipo
m[1,1] <- "hola" print(m)
se pueden asignar nombres a filas y columnas (y a las dimensiones correspondientes mediante
dimnames, pero eso implica usar listas, que se verán en el próximo apartado)> m <- matrix (1:9, 3) > dimnames(m) NULL > rownames(m) NULL > rownames(m) = letters[1:3] > colnames(m) = LETTERS[1:3] > m A B C a 1 4 7 b 2 5 8 c 3 6 9 > dimnames(m) [[1]] [1] "a" "b" "c" [[2]] [1] "A" "B" "C" > dimnames(m) <- list(Filas=rownames(m),Columnas=colnames(m)) > m Columnas Filas A B C a 1 4 7 b 2 5 8 c 3 6 9- ejercicio
- considera los datos
mtcars - estima los coeficientes de una regresión lineal de
mgpsobre el resto de variables \[\vec y = X \vec\beta + \vec\epsilon\qquad\epsilon\hookrightarrow\mathcal N(0,\sigma I)\] \[ \hat\beta = (X' X)^{-1} X' \vec y \] - compara el resultado con
lm(mpg ~ ., mtcars)
- considera los datos
4.2.2.2.2 Python
import numpy as npm = np.array ([[0,1,2], [3,4,5], [6,7,8]]) # a partir de lista de listasm = np.reshape (range(9), [3,3]) # igual al anterior; notar: empieza en 0 y rellena por filas- submatriz:
m[0:2,1:3] - primera fila:
m[0]; m[0,:] - primera columna:
m[:,0] - asignación:
m[1,2] = 11 - traspuesta:
np.transpose(m) from numpy.linalg import inv; inv(m)from numpy.linalg import det; det(m)np.dot (m, m)
4.2.2.3 listas
4.2.2.3.1 R
son como vectores pero, en cada celda, pueden contener cualquier objeto (incluso listas):
l <- list (a=23, b=1:5, c=m)
sublistas:
l[2] # lista de longitud 1 que contiene un vector; no es el vector l["b"] # idem l[c(1,3)] # sublista de longitud 2 l[c("a","c")] # idemextraer un elemento (no es lo mismo que una sublista de tamaño 1):
l[[3]] # la matriz l[[3]][,1] # l[3][,1] no funcionaría l[["c"]] # la matriz l$c # idem l$c[,1]
muchos de los objetos devueltos por funciones a alto nivel de R son listas
(regre <- lm(mpg ~ ., mtcars)) names(regre) regre$coefficients (sumario <- summary(regre)) names(sumario) sumario$r.squared (contraste.t <- t.test (mpg ~ am, mtcars)) names(contraste.t) str(contraste.t) ls.str(contraste.t) contraste.t$p.value # p-valor, nivel crítico
4.2.2.3.2 python
Se llama lista a las colecciones heterogéneas creadas con corchetes:
a = [1, 2, "hola", ["otra", "lista"]] a[0] # el primer elemento a[0:1] # una sublista que contiene sólo al primer elemento
Para usar etiquetas hace falta un diccionario…
v = {'beta': 88, 'alfa': 3, 'gama': -5} l = {"a":23, "b":v, "c":[1,2,3]} l["b"] # extraer un elemento l["b"]["alfa"] {i:l[i] for i in ["a","c"]} # subdiccionario
…o una Series de pandas:
import pandas as pd; L = pd.Series(l)
subseries:
L[[1]]; L[["b"]] L[[0,2]]; L[["a","c"]]
extraer un elemento:
L[1]; L["b"] L[1]["alfa"] L["b"]["alfa"]
4.2.2.4 dataframes
4.2.2.4.1 R
parecen matrices, con columnas heterogéneas (como las listas):
d <- data.frame (x = 1:5, y = c("uno","dos","tres","cuatro","cinco"), z = 11:15) d[3,2] # notación matricial para extraer elemento d[3,] # notación matricial para extraer fila (no hace "drop", sigue siendo un dataframe) d[,1] # notación matricial para extraer columna (hace "drop", es un vector) d[[1]] # notación de lista para extraer la primera columna (es un vector) d[c(1,3)] # notación de lista para extraer dos columnas d[,c(1,3)] # notación matricial para extraer dos columnas d$x # notación de lista para extraer columna por nombre d[["x"]] # notación de lista para extraer columna por nombreesta última versión se usa al programar con variables:
variable <- "x" summary(d[[variable]])
selección de casos mediante vectores lógicos:
d [d$x > 2, ] subset (d, x > 2) # para evitar repetir el nombre del dataframe subset (d, x > 2, y:z) # permite también rangos de columnas por nombre subset (d, , -z) # y usar "-" con los nombres de las variables subset (d, select=-z) subset (d, , -(y:z)) subset (d, , -c(x,z))
se pueden pegar verticalmente con
rbindrbind (d[3:5,], d[1:2,])
se pueden pegar horizantalmente con
cbindcbind (d[1:2,], d[3:4,])
- los dataframes son visibles desde
Rcmdr
4.2.2.4.2 Python
import pandas as pd
d = pd.DataFrame ({"x" : list(range(1,6)), "y" : ["uno","dos","tres","cuatro","cinco"]})
d.y
list (d.y)
d.y[2]
d["y"]
d[["y","x"]] ; d[[1,0]]
d.y [d.x > 3]; list (d.y [d.x > 3])
d [d.x > 3]
http://pandas.pydata.org/pandas-docs/stable/comparison_with_r.html
4.2.2.5 factores o categóricas
4.2.2.5.1 R
implementan variables cualitativas:
sexo <- c("M","M","H","H","H","M") sexo.f <- factor (sexo) levels (sexo.f)factorgenera un factors = c ("M", "M", "M", "H", "M", "H", "H", "HH", "HM") f = factor (s)un factor se parece a un vector de caracteres, pero no es:
as.character (f) as.numeric (f) nchar(s) # funciona nchar(f) # no
factortambién elimina los niveles sobrantesf1 = f[nchar(as.character(f))==1] f1 = factor(f1)
los
NAen principio no aparecen como niveles:factor(c(1,1,3,NA)) factor(c(1,1,3,NA),exclude=NULL)
para imponer un orden
factor (c("bien","mal","regular","bien")) factor (c("bien","mal","regular","bien"), levels=c("mal","regular","bien"))
4.2.2.5.2 Python
Quizá no tan básicos como en R.
implementan variables cualitativas:
import pandas as pd sexo = pd.Series(["M","M","H","H","H","M"]) sexo_f = sexo.astype("category") list(sexo_f.values.categories)para eliminar los niveles sobrantes
sexo_f2 = sexo_f[0:2] sexo_f2 = pd.Series(list(sexo_f2)).astype("category")los
nanno aparecen como niveles:import numpy as np pd.Series([1,1,3,np.nan]).astype("category")para imponer un orden
pd.Series (pd.Categorical (["bien", "mal", "regular", "bien"], categories = ["mal", "regular", "bien"]))
http://pandas.pydata.org/pandas-docs/stable/categorical.html
4.2.2.6 fechas y horas
4.2.2.6.1 R
Trasformar cadena en fecha:
as.Date ("1978-1-31") # 31 de enero de 1978Acepta formatos arbitrarios con estas plantillas:
plantilla representa %d día del mes %m mes (número) %b mes (abreviado) %B mes (nombre completo) %y año (dos cifras) %Y año (cuatro cifras) as Date ("31/1/78", format="%d/%m/%y") as.Date ("Ene 31, 1978", format="%b %d, %Y")Si el ordenador no está en español, para lo anterior habría que ejecutar antes:
Sys.setlocale ("LC_TIME", "es_ES.UTF-8")Asimismo, para leer fechas del sistema operativo (en idioma
POSIXoC) podría hacerse así:Sys.setlocale ("LC_TIME", "C") as.Date ("Jan 31, 1978", format="%b %d, %Y")Las fechas pueden restarse, o se les puede sumar o restar un entero.
as.Date ("1978-1-31") - as.Date ("1977-1-31") # podría aplicarse "as.numeric" as.Date ("1978-1-31") + 1Dada una fecha, el correspondiente día de la semana puede obtenerse con
weekdaysweekdays (as.Date ("1978-1-31"))Para pasar cadenas a horas, se usa
strptime:strptime ("Oct 10 07:44:31", format = "%b %d %H:%M:%S")Acepta plantillas
%H,%My%Spara horas minutos y segundo. Para otras, véase la ayuda destrptime.- Ejercicio
- Carga los datos ./dat/vacas.csv y calcula la edad al destete de cada vaca.
4.2.2.6.2 Python
Trasformar cadena en fecha:
import pandas as pd pd.Timestamp("2012-05-01") pd.Timestamp("1/1/1974") pd.Timestamp("31/1/78") pd.Timestamp("31/1/18") pd.Timestamp("2/1/18") # ojoLas fechas pueden restarse:
td = pd.Timestamp("2018-10-01") - pd.Timestamp("1976-02-09") td.total_seconds() / 86400 / 365.25Dada una fecha, el correspondiente día de la semana puede obtenerse:
fecha = pd.Timestamp("2018-10-01") fecha.weekday() fecha.weekday_nameTambién para horas acepta formatos variados:
pd.Timestamp("2012-05-01T12:30:15.3333333") pd.Timestamp("1-5-2012 12:30:15.3333333") # ojoPara pasar cadenas arbitrarias a horas, se puede usar
strptime:import time; time.strptime("Oct 10 07:44:31", "%b %d %H:%M:%S")Acepta plantillas
%H,%My%Spara horas minutos y segundo.
4.3 control
4.3.1 R
condicionales
Generemos un vector de temperaturas:
t <- runif (15, 10, 40)
Para combinar comparaciones vectorialmente, usamos
ifelsey un operador de circuito largo («&» = «y»; «|» = «ó»):ifelse (t>20 & t<30, "agradable", "desagradable")
Para combinar comparaciones de forma que esperamos un único booleano, usamos operadores de circuito corto («&&» = «y»; «||» = «ó»):
n=10; if (is.numeric(n) && length(n)==1 && n>0) sqrt(n) else "no puedo"
bloques de instrucciones mediante llaves «{}»; se usan en contextos donde tiene que ir más de una instrucción:
if (n > 5) {print("demasiado grande"); n<-5} else {print("demasiado pequeño"); n<-n+1}El valor devuelto por un bloque es el valor devuelto por su última instrucción.
bucles
for (i in 1:10) cat ("El cuadrado de", i, "es", i^2, "\n")Detrás de «in» puede ir cualquier vector o lista; por ejemplo
for (i in letters) {cat (i); cat (toupper (i)); cat ("-")}; cat ("\n") for (i in iris) print (summary (i))bucles con acumulador
Se define una variable (acumulador) antes del bucle para que recoja los resultados:
suma <- 0; for (i in 1:10) suma <- suma+i; suma # equivale a sum(1:10) -> suma producto <- 1; for (i in 1:10) producto <- producto*i; producto # prod(1:10); factorial(10) -> producto bector <- c(); for (i in 1:10) bector <- c(bector,i^2); bector # (1:10) ^ 2 -> bector lista <- list(); for (i in 1:10) lista <- c(lista,list(1:i)); lista # sapply (1:10, function (i) 1:i) -> lista
4.3.2 Python
condicionales
Para combinar comparaciones de forma que esperamos un único booleano, usamos operadores de circuito corto («and» = «y»; «or» = «ó»):
import math n=10 if ((isinstance(n,int) or isinstance(n,float)) and n>0): math.sqrt(n) else: "no puedo"
Generemos un vector de temperaturas:
import scipy.stats as st t = st.uniform.rvs (10, 40, 15)
Para combinar comparaciones vectorialmente, usamos
ifasí:["agradable" if ti>20 and ti<30 else "desagradable" for ti in t]
nótense los bloques de instrucciones tras dos puntos y con sangría:
if n > 5: print("demasiado grande") n = 5 else: print("demasiado pequeño") n++bucles
for i in range(10): print ("El cuadrado de", i, "es", i**2) mtcars = pd.read_csv ("http://bellman.ciencias.uniovi.es/cursoR/dat/mtcars.csv") for v in mtcars: mtcars[v].describe()bucles con acumulador
Se define una variable (acumulador) antes del bucle para que recoja los resultados:
numéricos
suma = 0 for i in range(1,11): suma += i
producto = 1 for i in range(1,11): producto *= i
recolección
vector = [] for i in range(1,11): vector.append (i**2)
lista = [] for i in range(10): lista.append (list (range (i)))
4.4 funciones
4.4.1 R
con nombre
f <- function(x) x^2 f(15)
anónimas (útiles para definiciones al vuelo, como se ve en la sección siguiente)
(function(x) x^2) (15)
pueden tener varios argumentos/parámetros y varias instrucciones en el cuerpo
var.ponderada <- function (x, pesos) # varianza ponderada { mp <- weighted.mean (x, pesos) # media ponderada weighted.mean ((x - mp) ^ 2, pesos) }cada argumento puede tener un valor por omisión
var.ponderada <- function (x, pesos = rep(1,length(x))) { mp <- weighted.mean (x, pesos) weighted.mean ((x - mp) ^ 2, pesos) }pueden pasar sus argumentos a otras funciones mediante «…»
var.ponderada <- function (x, pesos, ...) { mp <- weighted.mean (x, pesos, ...) weighted.mean ((x - mp) ^ 2, pesos, ...) }Por ejemplo:
muestra <- c (1, 20, NA, 5); pesos <- c (1,2,3,4) weighted.mean (muestra, pesos); weighted.mean (muestra, pesos, na.rm=TRUE) var.ponderada (muestra, pesos) # produce NA var.ponderada (muestra, pesos, na.rm=TRUE) # pasa «na.rm=TRUE» a weighted.mean
recursivas: una función puede llamarse a sí misma
mifactorial <- function(n) if (n==0) 1 else n*mifactorial(n-1)
otro ejemplo:
nombres <- c("Señor don Manuel Montenegro", "Asun Lubiano", "Doña Antonia Salas", "Don Norberto Corral", "Carlos Carleos") títulos <- c("don", "doña", "señor", "señora") ## dado un vector de nombres, obtener el primer nombre de pila de cada uno nombre.de.pila <- function(cadena) nombre.de.pila_vector (strsplit (cadena, " ") [[1]]) # convierte "cadena" en vector de palabras nombre.de.pila_vector <- function(v) # v = vector de cadenas { palabra1 <- v[1] if (tolower(palabra1) %in% títulos) # tolower = convierte a minúsculas nombre.de.pila_vector(v[-1]) # llamada recursiva else palabra1 } for (nombre in nombres) print (nombre.de.pila (nombre))
4.4.2 Python
con nombre
def f (x): return x**2 f(15)
anónimas (útiles para definiciones al vuelo, como se ve en la sección siguiente)
(lambda x: x**2) (15)
sólo pueden contener una expresión;
pueden tener varios argumentos
def media_ponderada (x, pesos): suma = 0 for i in range (len (x)): suma += x[i] * pesos[i] return suma / sum(pesos)cada argumento puede tener un valor por omisión
def media_ponderada (x, pesos = None): suma = 0 for i in range (len (x)): suma += x[i] * (pesos[i] if pesos else 1) return suma / (sum(pesos) if pesos else len(x))pueden pasar sus argumentos a otras funciones mediante un argumento con «*»
def var_ponderada (x, *otros): mp = media_ponderada (x, *otros) cuadrados = [(xi-mp)**2 for xi in x] return media_ponderada (cuadrados, *otros)
Por ejemplo:
muestra = [1, 20, 100, 5]; pesos = [1,2,3,4] media_ponderada (muestra) media_ponderada (muestra, pesos) var_ponderada (muestra) # pasa *otros como vacío var_ponderada (muestra, pesos) # pasa *otros como «pesos»
4.5 bucles sobre estructuras
4.5.1 R
- sobre secuencias (vectores o listas)
sapply(consde simple) se usa para generar un vector (o una matriz, si el resultado de la función aplicada es vectorial)sapply (1:10, sqrt) # aplicar una función con nombre; igual que sqrt(1:10) sapply (1:10, function(x) x**2) # aplicar una función anónima; igual que (function(x) x**2) (1:10) sapply (1:10, function(x) c(x^2,x^3)) # el resultado es una matriz; distinto de (function(x) c(x^2,x^3)) (1:10)
sapplyconserva etiquetas si se aplica a un vector de cadenassapply(3:5, sqrt) # sin etiquetas sapply(c("uno","dos","tres"), nchar) # con etiquetas structure (sapply(3:5, sqrt), names=3:5) # forzar etiquetaslapply(conlde lista) devuelve una listalapply (1:10, function(i) list (i, list(letters[i],month.name[i])))
aunque si se quieren conservar etiquetas mejor usar
sapplyo (si hace falta)sapply(..., simplify=FALSE)lapply (c ("uno", "dos", "tres"), nchar) sapply (c ("uno", "dos", "tres"), nchar) sapply (c ("uno", "dos", "tres"), nchar, simplify=FALSE)
applyse usa para aplicar una función a filas o columnas de una matriz…m <- matrix (1:12, 3) apply (m, 1, sum) # aplicar por filas apply (m, 2, sum) # aplicar por columnas
…o a un dataframe; en este caso, téngase en cuentra que se trasforma en matriz (homogénea) antes de aplicarse la función, por lo que (por ejemplo) si el dataframe contiene un factor todos los datos aparecen como cadenas:
## queremos trasformar todos los 4 de ChickWeight a NA ChickWeight cuatroNA <- function (x) {x[x==4] <- NA; x} cuatroNA (1:10) # funciona cuatroNA (as.character (1:10)) # funciona cuatroNA (factor (1:10)) # funciona summary (apply (ChickWeight, 2, cuatroNA)) # apply no funciona (trasforma todo a factores o cadenas) summary (data.frame (lapply (ChickWeight, cuatroNA))) # lapply sí funciona
es decir, cuando queremos aplicar una función a cada variable de un dataframe,
- es mejor considerar el dataframe como lista y usar
lapply - que considerar el dataframe como matriz y usar
apply(, 2,)
otro ejemplo usando la función
identity;identity(x)devuelvexmtcars apply(mtcars, 1, identity) # queda traspuesta apply(mtcars, 2, identity) identical(mtcars, data.frame (apply (mtcars, 2, identity))) # TRUE m <- mtcars m$am <- factor(m$am) apply(m, 1, identity) # genera matrices de cadenas apply(m, 2, identity) # idem identical(m, data.frame (apply (m, 2, identity))) # FALSE
- es mejor considerar el dataframe como lista y usar
para aplicar por grupos:
prod <- 1:20; sexo <- rep(c("M","H"),each=10) tapply (prod, sexo, mean) # por niveles de "sexo" by (prod, sexo, mean) # ídemla más general (mapeo)
mapply (rep, 1:4, 4:1) # aplica funciones con varios argumentos
un comando muy habitual en simulaciones:
replicate (10000, {m <- rnorm(5); mean(m)})Funciona parecido a
sapply (1:10000, function (i) {m <- rnorm(5); mean(m)})donde la variable
ies sintácticamente necesaria pero su valor no se usa.
4.5.2 Python
trasformación por descripción (mapeo)
from math import sqrt [sqrt(i) for i in range(10)] list (map (sqrt, range(10))) # lo mismo list (map (lambda x: x**2, range(10))) # con función anónima
otra versión de la media ponderada anteriormente definida:
def media_ponderada (x, pesos): return sum (map (lambda xi,pi: xi*pi, x, pesos)) / sum(pesos)
otra versión con argumento opcional:
def media_ponderada (x, pesos = None): return sum (map (lambda xi,pi: xi*pi, x, [1]*len(x) if pesos is None else pesos)) / (sum(pesos) if pesos else len(x))
aplicar una función a filas o columnas de un dataframe
from sklearn import datasets iris = datasets.load_iris() # datos de ejemplo import pandas as pd I = pd.DataFrame(iris.data, columns=iris.feature_names) I.apply(sum) # aplicar «sum» por columnas; equivale a I.sum() I.apply(sum,axis=0) # ídem I.apply(sum,axis=1) # aplicar «sum» por filas; equivale a I.sum(axis=1)
para aplicar por grupos:
I["especie"] = pd.Series(pd.Categorical.from_codes(codes=iris.target,categories=iris.target_names)) I.groupby("especie").apply(lambda x: x.iloc[:,0:4].median()) # 0:4 para evitar "especie"
5 Estadística básica programando
5.1 Obtener datos
5.1.1 R
5.1.1.1 De ejemplo (incluidos en la distribución de R)
Listar los disponibles:
data ()
En una sesión de R básico (sin Rcmdr) están disponibles varios dataframes, como «mtcars». Para otros hay que cargar la biblioteca correspondiente; por ejemplo:
library (car) # para datos «Chile» summary (Chile)
En una sesión de Rcmdr se ocultan los dataframes de ejemplo para que no molesten en la lista de datos disponibles. Para trabajar con tales datos hay que cargar la biblioteca «datasets»:
library (datasets)
5.1.1.2 En formato nativo de R
- Habitualmente, el fichero con datos nativos tiene extensión
.rdaó.RData. - Pueden contener
- un solo conjunto de datos (cuyo nombre puede coincidir o no con el nombre del fichero)
- múltiples conjuntos de datos, además de variables, funciones, etc. (entorno de trabajo de R)
Se carga con
load:getwd () # ruta del directorio de trabajo load ("mi-fichero.rda") # en el directorio de trabajo load ("~/Documentos/datos/mi-fichero.rda") # en otro directorio, necesita ruta setwd ("~/Documentos/datos") # cambiar directorio de trabajo # puede usarse una URL como ruta: load (url ("http://bellman.ciencias.uniovi.es/cursoR/dat/mtcoches.rda")) ls () # aparece mtcoches head (mtcoches)
5.1.1.3 En formatos ajenos
(Lo mismo en Python.)
- De especial interés es la importación de datos de texto (CSV)
codificación: utf-8 (unicode) o latin-1 (iso-8859-1, -15)
datos <- read.table (........., encoding = "latin1") # para ISO-8859-1, originados en Windows habitualmente datos <- read.table (........., encoding = "UTF-8") # codificación más habitual para datos Unicode
- a partir de la versión 4 de R, en las siguientes órdenes (read.csv2, read.table, read.fwf)
puede interesar usar la opción
stringsAsFactors=TRUE - campos
delimitados por un carácter solo (vacas.csv)
vacas1 <- read.csv2 (url ("http://bellman.ciencias.uniovi.es/cursoR/dat/vacas.csv"))delimitados por varios espacios en blanco (sin espacios dentro de campo: vacas.txt; con espacios: vacas.blancos1)
vacas2 <- read.table (url ("http://bellman.ciencias.uniovi.es/cursoR/dat/vacas.txt"), header=TRUE) vacas3 <- read.table (url ("http://bellman.ciencias.uniovi.es/cursoR/dat/vacas.blancos1"), head=TRUE)columnas de anchura fija (vacas.blancos2)
direccion <- "http://156.35.96.172/cursoR/dat/vacas.blancos2" variables <- strsplit (readLines(url(direccion), n=1), " +") [[1]] ## " +" significa "uno o más espacios" vacas4 <- read.fwf (url(direccion), rep(30,11), skip=1, stringsAsFactors=TRUE) names(vacas4) <- variables for (i in which(sapply(vacas4,is.factor))) levels(vacas4[,i]) <- trimws(levels(vacas4[,i]))
5.1.2 Python
5.1.2.1 De ejemplo (incluidon en python-sklearn)
from sklearn import datasets iris = datasets.load_iris()
5.1.2.2 En formato nativo de Python (pickle)
Cualquier objeto de Python, incluyendo los dataframes de Pandas, puede serializarse (guardarse en un fichero):
import pandas as pd
d = pd.DataFrame({'a':[1,2,3,4,5],'b':["uno","uno","onu","onu","uno"]})
d.to_pickle("/tmp/fichero.dat")
Para leer un dataframe de un fichero pickle:
datos = pd.read_pickle ("/tmp/fichero.dat")
5.1.2.3 En formatos ajenos
(Lo mismo en R.)
Importar Pandas
import pandas as pd
- Para datos de texto (CSV) hay
read_csv()(comas) yread_table()(tabuladores)codificación: utf-8 (unicode) o latin-1 (iso-8859-1, -15)
datos = pd.read_table (........., encoding = "latin1") # para ISO-8859-1, originados en Windows habitualmente datos = pd.read_table (........., encoding = "UTF-8") # codificación más habitual para datos Unicode
- ¿campos delimitados o de anchura fija?
delimitados por un carácter solo (vacas.csv)
vacas1 = pd.read_csv ("http://bellman.ciencias.uniovi.es/cursoR/dat/vacas.csv", sep=";", encoding="utf-8")delimitados por varios espacios en blanco (sin espacios dentro de campo: vacas.txt)
vacas2 = pd.read_table ("http://bellman.ciencias.uniovi.es/cursoR/dat/vacas.txt", sep='\s+', engine='python')columnas de ancho fijo (vacas.blancos2)
vacas5 = pd.read_fwf ("http://156.35.96.172/cursoR/dat/vacas.blancos2", widths = [30] * 11)
Para datos con fechas, opción
parse_dates:vacas5 = pd.read_fwf ("http://156.35.96.172/cursoR/dat/vacas.blancos2", widths = [30] * 11, parse_dates=[1,2]) # fechas en columnas segunda y tercera
5.2 Guardar datos
5.2.1 R
Guardar todo el entorno de trabajo (funciones, dataframes…)
save.image () # lo guarda en ./.RData (el fichero cargado al arrancar R) save.image (file = "~/trabajo/mi-sesión.rda") # en fichero arbitrario
Guardar uno o varios objetos en formato nativo de R
save (mi.dataframe, mi.función, file = "~/trabajo/mis-objetos.rda")
Guardar un dataframe como una tabla de texto (CSV)
write.table (mtcars, "/tmp/mtcars1.csv") # sep=" " dec="." sin campo de rownames en cabecera write.csv (mtcars, "/tmp/mtcars2.csv") # sep="," dec="." write.csv2 (mtcars, "/tmp/mtcars3.csv") # sep=";" dec=","
5.2.2 Python
Guardar entorno de trabajo
import dill dill.dump_session ("/tmp/miTrabajo.pkl") # recuperar con dill.load_sessionGuardar un objeto en formato nativo de Python
misDatos.to_pickle ("/tmp/misDatos.pkl")Guardar un dataframe como una tabla de texto (CSV)
misDatos.to_csv ("/tmp/misDatos.csv")
5.3 Descriptivos
5.3.1 R
D <- mtcars # dataframe de ejemplo D$am <- factor (mtcars$am) # una cualitativa; también: D$am <- factor(D$am, labels=c("auto","manual")) summary (D) # resumen del dataframe T <- table (D$cyl) # frecuencias absolutas prop.table (T) # frecuencias relativas summary (D$hp) # media y cinco cuartiles mean (D$hp) # media var (D$hp) # varianza sd (D$hp) # desvío típico median (D$hp) # mediana quantile (D$hp, 0.95) # percentil 95 quantile (D$hp, 0:4/4) # cinco cuartiles; similar a fivenum(D$hp) IQR (D$hp) # recorrido intercuartílico
En muchas funciones se puede incluir la opción na.rm=TRUE para omitir los ausentes:
mean (c (1:10, NA)) mean (c (1:10, NA), na.rm=TRUE)
Gráficas:
barplot (table (D$cyl)) # diagrama de barras pie (table (D$am)) # diagrama de sectores hist (D$hp) # histograma boxplot (hp ~ am, D) # diagrama de cajas plot (mpg ~ hp, D) # diagrama de dispersión (nube de puntos) pdf ("fichero.pdf") # guarda gráficas subsiguientes en 1 fichero PDF (vectorial) for (i in 1:ncol(mtcars)) { if (is.numeric (mtcars[[i]])) hist (mtcars[[i]]) else barplot (table (mtcars[[i]])) } dev.off () # cierra el PDF png ("fichero%d.png") # guarda gráficas subsiguientes en ficheros PNG (pixelados) for (i in 1:3) boxplot (mtcars[[i]] ~ mtcars$am) dev.off () # cierra el PNG
Ejercicio:
Escribir un programa en R que realice gráficas adecuadas para las variables del conjunto de datos «Chile» del paquete «car».
data (Chile, package="car") Chile$education <- factor (Chile$education, levels=c("P","S","PS"))
5.3.2 Python
Con los datos clásicos de flores iris:
import pandas as pd i = pd.read_csv ("datos/iris.csv") i.describe() # numérico i["Species"].describe() # moda iSn = i['Species'].value_counts() # recuentos iSn / iSn.sum() # frecuencias relativas i["Petal.Length"].mean() # media i["Petal.Length"].var() # varianza i["Petal.Length"].std() # desvío típico i["Petal.Length"].median() # mediana i["Petal.Length"].quantile(0.5) # ídem i["Petal.Length"].quantile([.05,.95]) # percentiles 5 y 95 import numpy as np # para «nan» pd.Series([1,2,np.nan,4]).mean() # excluye los ausentes
Gráficas:
import matplotlib.pyplot as plt i["Petal.Length"].plot(kind="hist") # histograma plt.show() # mostrar en pantalla i["Petal.Length"].value_counts().plot(kind="bar") # diagrama de barras plt.savefig("barras.png") # guardar en fichero i["Petal.Length"].value_counts().plot(kind="pie") # diagrama de sectores i["Petal.Length"].plot(kind="box") # diagrama de caja i.boxplot("Petal.Length","Species") # cajas por grupo
5.4 Modificar datos
5.4.1 R
Crear nueva variable de un dataframe:
mtcars$consumo <- (3.8 / mtcars$mpg * 1.6) * 100
Recodificar:
mtcars$am <- factor (mtcars$am, labels=c("auto","manual")) mtcars$consumo3 <- cut (mtcars$consumo, c(-Inf, 10, 20, 30, Inf), c("muy poco", "poco", "mucho", "demasiado"))Reordenar niveles de factor:
data (Chile, package="car") Chile$educación <- factor (Chile$education, levels = c("P","S","PS")) # P=primaria, S=secundaria, PS=postsecundariaFiltrar
edades.mujeres <- Chile$age [Chile$sex == "F"] mtcars4v <- mtcars [mtcars$cyl==4 & mtcars$vs==0, ] ?== # ayuda sobre < > == != ?& # ayuda sobre ! & |
5.4.2 Python
import pandas as pd
Chile = pd.read_csv ("http://bellman.ciencias.uniovi.es/cursoR/dat/Chile.csv")
Crear nueva variable en un dataframe:
Chile.euro = 1.2 * Chile.income
Recodificar:
Chile.sexo = Chile.sex.astype("category") Chile.sexo.values.categories = ["mujer", "varón"] Chile.clase = pd.cut (Chile.income, [-np.inf,30000,100000,np.inf], labels=["baja","media","alta"])Reordenar niveles de categórica:
Chile["educación"] = Chile["education"].astype("category",categories=["P","S","PS"])Filtrar:
edades_mujeres = Chile.age[Chile.sex=="F"] varones_jovenes = Chile[(Chile.sex=="M") & (Chile.age<35)]
Más en la documentación de Pandas.
5.5 Distribuciones de probabilidad
5.5.1 R
- letra inicial
rpara generar aleatoriosppara la función de distribución \(F_X\,(t) = \Pr\,[X\leq t]\)dpara la función de densidad de variables continuas o la función de probabilidad (o de cuantía, o de masa) de variables discretas \(f_X\,(t) = \Pr\,[X=t]\)qpara la función cuantil
- abreviatura del nombre de la familia de la distribución
unifuniformenormgausianaexpexponencialbinombinomialpoisPoissontStudentchisq\(\chi^2\) (ji-cuadrado)
runif (10, 0, 1) # genera 10 aleatorios con distribución uniforme entre 0 y 1 pnorm (150, 170, 15) # probabilidad de que una gausiana N(170;15) sea menor que 150 plot (x <- seq(0,5,.1), dexp(x,1)) # curva de densidad de una exponencial con media 1 qpois (0.5, 1.7) # mediana de una distribución de Poisson con media 1,7
5.5.2 Python
- métodos
rvspara generar aleatorioscdffunción de distribución (cumulative density function)pdffunción de densidad (probability density function)pmffunción masa de probabilidad (probability mass function)mean,var,std,median- media, varianza, desvío típico, medianappffunción cuantil (percent point function)
- distribuciones
uniformuniformenormgausianaexponexponencialbinombinomialpoisPoissontStudentchi2ji-cuadrado (\(\chi^2\))
import scipy.stats as st st.uniform.rvs (2, 0.1, 30) # 30 valores uniformes entre 2 y 2+0,1 st.norm.cdf (200, 170, 10) # función de distribución en 200 de una N(170;10) import matplotlib.pyplot as plt # función de densidad (de la docstring de expon) fig, ax = plt.subplots(1, 1) x = np.linspace(expon.ppf(0.01), expon.ppf(0.99), 100) ax.plot(x, expon.pdf(x), 'r-', lw=5, alpha=0.6, label='exponencial') ## también se pueden fijar previamente los parámetros: v = st.binom (10, .3) # binomial n=10, p=0,3 v.mean(), v.var(), v.std() # media, varianza, desvío típico v = st.poisson (100) # puasón con media 100 v.ppf([.05,.95]) # percentiles 5 y 95
5.6 Contrastes de hipótesis sobre medias, proporciones…
5.6.1 R
?cars # velocidad y distancia de frenada library (car) # para datos Chile ## contraste de gausianidad shapiro.test (cars$speed) # comprobar mediante stem o hist shapiro.test (Chile$statusquo) shapiro.test (Chile$age) ## información del objeto "contraste" shapiro.test (cars$speed) -> contraste names (contraste) # "statistic" "p.value" "method" "data.name" contraste$p.value # nivel crítico o p-valor ## simulación n <- 100 # tamaño muestral m <- rnorm(n); stem(m); shapiro.test(m)$p.value # relación entre forma y p-valor mean (replicate (10000, shapiro.test(rnorm(n))$p.value) < 0.05) # proporción de rechazos ## contraste sobre la media t.test (cars$speed, mu=15) # bilateral t.test (cars$speed, mu=15, alternative="less") # H0: mu=15; H1: mu<15 t.test (cars$speed, mu=15, alternative="greater") # H0: mu=15; H1: mu>15 ## contraste sobre proporción summary (Chile$sex) ?prop.test prop.test (sum(Chile$sex=="F"), nrow(Chile), 0.5) # H0: p = 1:2; H1: p =/= 1:2 ## contraste sobre la mediana wilcox.test (cars$speed, mu=15) # bilateral wilcox.test (cars$speed, mu=15, alternative="less") # H0: mu=15; H1: mu<15 wilcox.test (cars$speed, mu=15, alternative="greater") # H0: mu=15; H1: mu>15 M <- rexp (25) # exponencial con media=1 Me <- qexp (.5) # mediana teórica = 0,693.147.2 wilcox.test (M, mu=Me) # poco recomendable porque exige simetría mean (replicate (100000, {M <- rexp(25); wilcox.test(M,mu=Me)$p.value<.05})) # 11% en vez de 5% prop.test (sum(M>Me), 25, .5) # prueba de signos: poco potente, pero cumple mean (replicate (100000, {M <- rexp(25); prop.test(sum(M>Me),25,.5)$p.value<.05})) # <5% mean (replicate (100000, {M <- rexp(25); t.test(M,mu=1)$p.value<.05})) # 7,5% (pero con media, no mediana) ## contraste sobre dos proporciones ## ¿es significativamente mayor la proporción de mujeres que votan Y? ## p = proporción que votan Y; H0: pF=pM; H1: pF>pM mujeres <- Chile [Chile$sex=="F" & !is.na(Chile$vote),] varones <- Chile [Chile$sex=="M" & !is.na(Chile$vote),] prop.test (c (sum (mujeres$vote=="Y"), sum (varones$vote=="Y")), c (nrow (mujeres), nrow (varones)), alternative = "greater") ## contraste de igualdad de varianzas (auxiliar para el de igualdad de medias) ? iris # comparar varianza de Petal.Length en «versicolor» y «virginica» with (iris, plot (Petal.Length, Petal.Width, col=Species)) boxplot (Petal.Length ~ Species, iris) with (iris, by (Petal.Length, Petal.Species, shapiro.test)) PLversicolor <- iris [iris$Species=="versicolor", "Petal.Length"] PLvirginica <- iris [iris$Species=="virginica", "Petal.Length"] var.test (PLversicolor, PLvirginica) # contraste de igualdad de varianzas var.test (Petal.Length ~ Species, iris, subset = Species %in% c("versicolor","virginica")) # lo mismo bartlett.test (Petal.Length ~ Species, iris, subset = Species %in% c("versicolor","virginica")) # otro similar ## contraste de igualdad de medias (muestras independientes) t.test (Petal.Length ~ Species, iris, subset = Species %in% c("versicolor","virginica")) # estimando dos varianzas distintas t.test (Petal.Length ~ Species, iris, subset = Species %in% c("versicolor","virginica"), var.equal = TRUE) # casi no cambia el p-valor ## contraste de igualdad de medias (muestras pareadas) ? ChickWeight # ¿Hay incremento significativo de peso a partir del día 20? boxplot (weight ~ Time, ChickWeight) cw <- ChickWeight [ChickWeight $ Time %in% c (20, 21), ] t.test (weight ~ Time, cw, alternative="less") # como si fueran independientes cw20 <- cw [cw$Time == 20,]; rownames(cw20) <- cw20$Chick cw21 <- cw [cw$Time == 21,]; rownames(cw21) <- cw21$Chick ambos <- intersect (rownames(cw20), rownames(cw21)) incremento <- cw21[ambos,"weight"] - cw20[ambos,"weight"] shapiro.test (incremento) # innecesario por el tamaño de muestra (45) t.test (cw20[ambos,"weight"], cw21[ambos,"weight"], paired=TRUE, alternative="less") t.test (incremento, mu=0, alternative="greater") # equivale al anterior ## contraste sobre la mediana de la diferencia (muestras independientes) ## comparar Petal.Width en «setosa» y «virginica» dentro del conjunto de datos «iris» ?iris shapiro.test (iris [iris$Species == "setosa", "Petal.Width"]) shapiro.test (iris [iris$Species == "versicolor","Petal.Width"]) t.test (Petal.Width ~ Species, iris, subset = Species %in% c("setosa","versicolor")) # suficiente tamaño muestral wilcox.test (Petal.Width ~ Species, iris, subset = Species %in% c("setosa","versicolor")) # resultado parecido ## contraste sobre la mediana de la diferencia (muestras pareadas) ?sleep # ¿hay diferencias significativas en sueño extra según somnífero? boxplot (extra ~ group, sleep) extra1 <- sleep$extra [sleep$group == '1'] extra2 <- sleep$extra [sleep$group == '2'] dif <- extra1 - extra2 shapiro.test (dif) wilcox.test (extra1, extra2, paired=TRUE) # asegurarse de que el orden se corresponde en ambos vectores wilcox.test (sleep ~ group, sleep, paired=TRUE) # otra forma de expresarlo wilcox.test (dif) # es equivalente a un contraste de Wilcoxon de 1 muestra t.test (extra1, extra2, paired=TRUE) # no muy distinto
- Otro ejemplo:
Comparar las dos secuencias «x» y «y» de seudoaleatorios de cierto generador. Cada valor de «y» es el consecutivo (dentro de la secuencia seudoaleatoria) del correspondiente en «x».
?randu dif <- randu$x - randu$y # comparar con el siguiente seudoaleatorio shapiro.test (dif) # irrelevante por el tamaño muestral, en principio... wilcox.test (randu$x, randu$y, paired=TRUE) t.test (randu$x, randu$y, paired=TRUE) # ...pero p-valor cerca del 5% ## comparar con seudoaleatorios decentes xy <- matrix(runif(400*5),400,byrow=TRUE)[,1:2]; x <- xy[,1]; y <- xy[,2] wilcox.test (x, y, paired=TRUE)
5.6.2 Python
import numpy as np # para nan, isnan import pandas as pd # para dataframes from scipy import stats # para contrastes import matplotlib.pyplot as plt # para histograma cars = pd.read_csv ("http://bellman.ciencias.uniovi.es/cursoR/dat/cars.csv") Chile = pd.read_csv ("http://bellman.ciencias.uniovi.es/cursoR/dat/Chile.csv") ## contraste de gausianidad stats.shapiro (cars.speed) stats.shapiro (cars.speed) [1] # p-valor stats.shapiro (Chile.age [~ np.isnan (Chile.age)]) # hay NA ## simulación n = 100 # tamaño muestral ## relación entre forma y p-valor m = stats.norm.rvs(0,1,n); m.plot(kind="hist"); plt.show(); stats.shapiro(m)[1] (pd.Series([stats.shapiro(stats.norm.rvs(0,1,n))[1] for i in range(10)]) < 0.05) . mean() # proporción de rechazos ## contraste sobre la media pvalor2 = stats.ttest_1samp (cars.speed, 15) . pvalue # bilateral ## ya que mediamuestral = 15,4 > 15 entonces pvalor1 = pvalor2 / 2 # unilateral H0: mu=15; H1: mu>15 1 - pvalor1 # unilateral H0: mu=15; H1: mu<15 ## contraste sobre proporción H0: p = 1:2; H1: p =/= 1:2 Chile.sex.value_counts() n = Chile.sex.count() p = Chile.sex.value_counts(True)['F'] from math import sqrt 2 * (1 - stats.norm.cdf (abs ((p - 0.5) / sqrt (0.25/n)))) # p-valor bilateral stats.chisquare ([1379,1321]) . pvalue # otra posibilidad: usar contraste ji-2 equivalente ## contraste sobre la mediana M = stats.expon.rvs (0, 1, 25) # exponencial con media=1 Me = stats.expon.ppf (.5) # mediana teórica = 0,693.147.2 stats.wilcoxon (M - Me) # poco recomendable porque exige simetría nM = sum (M-Me > 0); stats.chisquare ([nM, len(M)-nM]) # prueba de signos: poco potente ## contraste sobre dos proporciones ## ¿es significativamente mayor la proporción de mujeres que votan Y? ## p = proporción que votan Y; H0: pF=pM; H1: pF>pM tabla = Chile.groupby(['sex','vote']).size().unstack() # tabla de contingencia stats.chi2_contingency(tabla)[1] # P-valor de contraste ji-2 de homogeneidad mujeres = Chile [(Chile.sex=="F") & ~pd.isnull(Chile.vote)] varones = Chile [(Chile.sex=="M") & ~pd.isnull(Chile.vote)] pvalor2 = stats.chi2_contingency([[sum(varones.vote=="Y"),sum(varones.vote!="Y")], [sum(mujeres.vote=="Y"),sum(mujeres.vote!="Y")]]) [1] pF = sum(mujeres.vote=="Y")/len(mujeres) # 37% pM = sum(varones.vote=="Y")/len(varones) # 32% pvalor1 = pvalor2 / 2 # porque pF > pM ## contraste de igualdad de varianzas (auxiliar para el de igualdad de medias) ## ¿hay diferencias significativas en sueño extra entre los dos grupos? sleep = pd.read_csv ("http://bellman.ciencias.uniovi.es/cursoR/dat/sleep.csv") stats.shapiro (sleep.extra [sleep.group == 1]) stats.shapiro (sleep.extra [sleep.group == 2]) stats.bartlett (sleep.extra [sleep.group == 1], sleep.extra [sleep.group == 2]) ## contraste de igualdad de medias (muestras independientes) stats.ttest_ind (sleep.extra [sleep.group == 1], sleep.extra [sleep.group == 2]) # suponiendo varianzas iguales stats.ttest_ind (sleep.extra [sleep.group == 1], sleep.extra [sleep.group == 2], equal_var=False) ## contraste de igualdad de medias (muestras pareadas) ## ¿hay incremento significativo de peso a partir del día 20? CW = pd.read_csv ("http://bellman.ciencias.uniovi.es/cursoR/dat/ChickWeight.csv") CW.boxplot ("weight", "Time") plt.show() CW.weight[CW.Time==20].mean() # menor CW.weight[CW.Time==21].mean() # mayor stats.ttest_ind (CW.weight[CW.Time==20], CW.weight[CW.Time==21]).pvalue/2 # como si fueran independientes cw = CW[CW.Time.isin([20,21])] cw20 = cw [cw.Time == 20]; cw20.index = cw20.Chick cw21 = cw [cw.Time == 21]; cw21.index = cw21.Chick ambos = cw20.index.intersection(cw21.index) stats.shapiro (cw20.loc[ambos,"weight"] - cw21.loc[ambos,"weight"]) # innecesario por el tamaño de muestra (45) stats.ttest_rel (cw20.loc[ambos,"weight"], cw21.loc[ambos,"weight"]).pvalue / 2 ## contraste sobre la mediana de la diferencia (muestras independientes) ## comparar Petal.Width en «setosa» y «virginica» dentro del conjunto de datos «iris» iris = pd.read_csv ("http://bellman.ciencias.uniovi.es/cursoR/dat/iris.csv") stats.shapiro (iris.loc[iris.Species == "setosa", "Petal.Width"]) stats.shapiro (iris.loc[iris.Species == "virginica", "Petal.Width"]) stats.ttest_ind (iris.loc[iris.Species=="setosa","Petal.Width"], iris.loc[iris.Species=="virginica","Petal.Width"], equal_var=False) stats.mannwhitneyu (iris.loc[iris.Species=="setosa","Petal.Width"], iris.loc[iris.Species=="virginica","Petal.Width"], alternative='two-sided') # parecido ## contraste sobre la mediana de la diferencia (muestras pareadas) randu = pd.read_csv ("http://bellman.ciencias.uniovi.es/cursoR/dat/randu.csv") # comparar «x» con «y» dif = randu.x - randu.y stats.shapiro (dif) # irrelevante por el tamaño muestral stats.wilcoxon (dif) stats.wilcoxon (randu.x, randu.y) # otra forma de hacer lo mismo stats.ttest_rel (randu.x, randu.y) # parecido stats.ttest_1samp (dif, 0) # lo mismo
5.7 Contrastes de hipótesis sobre independencia
5.7.1 R
library(car) # para Chile ### contraste ji-2 ## ¿hay relación entre región y sexo? table (Chile$region, Chile$sex) prop.table(table (Chile$region, Chile$sex), 1) chisq.test (table (Chile$region, Chile$sex)) ## ¿hay relación entre educación y sexo? ## ¿hay relación entre sexo y voto? ## ¿hay relación entre educación y voto? ### contraste de correlación lineal ## ¿hay relación entre población, edad, ingresos y statusquo? variables <- c("population", "age", "income", "statusquo") # names (which (sapply (Chile, is.numeric))) cor (Chile[variables], use="pair") sapply (Chile[variables], shapiro.test) # no gausianas => mejor Spearman plot (Chile$population, Chile$age) cor.test (Chile$population, Chile$age) # por omisión, Pearson (exige gausianidad) cor.test (Chile$population, Chile$age, method="spearman") plot (Chile$population, Chile$income) plot (jitter(Chile$population), jitter(Chile$income)) # jitter ayuda para representar discretas con pocos niveles ## etc.
5.7.2 Python
import numpy as np # para isnan import pandas as pd from scipy import stats import matplotlib.pyplot as plt # para scatter Chile = pd.read_csv ("http://bellman.ciencias.uniovi.es/cursoR/dat/Chile.csv") ### contraste ji-2 ## ¿hay relación entre región y sexo? tabla = Chile.groupby(["region","sex"]).size().unstack() tabla = pd.crosstab (Chile.region, Chile.sex) # otra forma pd.crosstab (Chile.region, Chile.sex, normalize="index") # index=filas columns=columnas stats.chi2_contingency (tabla) ## ¿hay relación entre educación y sexo? ## ¿hay relación entre sexo y voto? ## ¿hay relación entre educación y voto? ### contraste de correlación lineal ## ¿hay relación entre población, edad, ingresos y statusquo? Chile.corr() variables = ["population", "age", "income", "statusquo"] Chile[variables].apply(stats.shapiro) # pero hay «nan»es Chile[variables].apply(lambda x:stats.shapiro(x[~np.isnan(x)])) # no gausianas => mejor Spearman plt.scatter (Chile.population, Chile.age) def cor_test (x, y): xsinnan = ~ np.isnan (x) ysinnan = ~ np.isnan (y) ambos = xsinnan & ysinnan return stats.pearsonr (x[ambos], y[ambos]) cor_test (Chile.population, Chile.age) # pearson stats.spearmanr (Chile.population, Chile.age) # spearman ## etc.
5.8 Regresión lineal
5.8.1 R
cor (mtcars) # buscamos predictor para «mpg» sort (abs (cor(mtcars)[,"mpg"])) # el peso parece el mejor predictor lineal plot (mpg ~ wt, mtcars) modelo <- lm (mpg ~ wt, mtcars) abline (modelo, col=2, lwd=3) # añade recta; lwd = linewidth = anchura summary (modelo) # coeficientes, R2, p-valor, estima de sigma ## p-valor del modelo = p-valor de la pendiente predict (modelo, data.frame(wt=3)) # para un coche de 3.000 libras coef(modelo) %*% c(1,3) # lo mismo; 1 multiplica al intercepto
5.8.2 Python
import pandas as pd mtcars = pd.read_csv ("http://bellman.ciencias.uniovi.es/cursoR/dat/mtcars.csv") mtcars.corr() abs(mtcars.corr().mpg).sort_values() # «wt» parece el mejor predictor lineal import matplotlib.pyplot as plt x = mtcars.wt; y = mtcars.mpg x = x.values.reshape(-1,1); y = y.values.reshape(-1,1) plt.scatter (x, y) plt.show() from sklearn import linear_model regre = linear_model.LinearRegression() regre.fit (x, y) plt.scatter (x, y) plt.plot (x, regre.predict (x), color='red', linewidth=3) plt.show() regre.predict(3) # predicción para 3.000 libras regre.intercept_ + regre.coef_ * 3 # lo mismo regre.score (x, y) # R2
Con otro módulo (quizá requiera «apt install python-statsmodels»):
import pandas as pd mtcars = pd.read_csv ("http://bellman.ciencias.uniovi.es/cursoR/dat/mtcars.csv") import statsmodels.formula.api as smf regre = smf.ols ("mpg ~ wt", data = mtcars) resul = regre.fit() print (resul.summary ()) print (resul.summary2 ()) # incluye estimación de varianza residual (scale)
6 Lenguaje: avanzado
6.1 comentarios
- si se escribe el carácter almohadilla «#» todo lo que queda a su derecha en el mismo renglón no se evalúa
se usa para introducir comentarios en código fuente de R
help("if") # sirve para buscar la ayuda asociada a la orden "if"otro uso frecuente es para desactivar parte de un programa
# desactivo temporalmente lo relativo a la variable "z" x <- 10 y <- 15 # z <- 34 x + y # + z
- hay cierta tradición de usar varias almohadillas para indicar estructura
una sola para comentarios en el mismo renglón, o sangrados bien a la derecha
log(dnorm(x)) # es más eficiente usar dnorm(X,log=TRUE) # véase ?dnormdos almohadillas para comentarios con misma sangría que el código
## bucle principal for (i in 1:10) { i2 <- i * 2 ## mostramos el resultado al usuario cat (i,"por dos es igual a",i2,"\n")tres o más almohadillas para comentarios sin sangría, habitualmente para señalar una sección importante del código
### bibliotecas necesarias library (rpart) # para árboles de regresión ## si la siguiente falla, instálese mediante install.packages("mvtnorm") library (mvtnorm) ### programa principal ...
6.2 variables
todo objeto del lenguaje R puede almacenarse en una variable
radio <- 10 # asignamos el valor '10' a la variable 'radio' radio # para comprobar el valor almacenado radio = 20 # otra forma de asignar 30 -> radio # otra forma de asignar assign ("radio", 40) # otra forma de asignar
- el operador habitualmente recomendado para asignar en programas es
<- - el operador «=» se usa también para asignar valores a argumentos de funciones, por lo que su uso puede resultar ambiguo
la función
assignse usa sobre todo si el nombre de la variable se determina durante la ejecución del programafor (i in 1:3) assign(paste0("x",i),i*2) # equivale a x1 <- 2; x2 <- 4; x3 <- 6a la inversa, para obtener el valor de una variable a partir de una cadena se usa
getsummary (mtcars) # bien summary ("mtcars") # no es lo que queremos summary (get ("mtcars")) # bien datos <- "mtcars" summary (get (datos)) # bienen raras ocasiones puede interesas modificar una variable perteneciente a un "entorno exterior"; para ello se usa el símbolo
<<-> a <- 3 > incrementar.a <- function () a <- a+1 > incrementar.a() > a [1] 3 > incrementar.a <- function () a <<- a+1 > incrementar.a() > a [1] 4
- el operador habitualmente recomendado para asignar en programas es
para conocer qué variables hay definidas en cierto momento
ls()
para borrar la definición de una variable se puede usar alguna de estas dos formas
rm (radio) rm (list = "radio")
si se quieren eliminar todas las variables definidas hasta el momento
rm (list = ls())
6.3 tipos de datos
6.3.1 números
representación
redondeo
floor(pi) # por abajo ceiling(pi) # por arriba round(pi) # redondeo a entero round(pi,3) # redondeo a milésimas round(max(mtcars$hp),-2) # redondeo a centenas signif(c(pi,1/3), 3) # cifras significativas formatC(5, width=10, flag="0") # forzar anchura; rellenar con ceros
coma decimal
options()$OutDec # por omisión, punto options("OutDec") options(OutDec=",") 1/3 options(OutDec="'") 1e-3
6.3.2 cadenas
representación en gráficas
abbreviate: recorta automáticamente de forma inambigua
> abbreviate(rownames(mtcars)) Mazda RX4 Mazda RX4 Wag Datsun 710 Hornet 4 Drive "MRX4" "MRXW" "D710" "Hr4D" Hornet Sportabout Valiant Duster 360 Merc 240D "HrnS" "Vlnt" "D360" "M240" Merc 230 Merc 280 Merc 280C Merc 450SE "M230" "Mr280" "M280C" "M450SE" Merc 450SL Merc 450SLC Cadillac Fleetwood Lincoln Continental "Mr450SL" "M450SLC" "CdlF" "LncC" Chrysler Imperial Fiat 128 Honda Civic Toyota Corolla "ChrI" "F128" "HndC" "TytCrl" Toyota Corona Dodge Challenger AMC Javelin Camaro Z28 "TytCrn" "DdgC" "AMCJ" "CZ28" Pontiac Firebird Fiat X1-9 Porsche 914-2 Lotus Europa "PntF" "FX1-" "P914" "LtsE" Ford Pantera L Ferrari Dino Maserati Bora Volvo 142E "FrPL" "FrrD" "MsrB" "V142"
6.3.3 tensores / arreglos
matrices multidimensionales (array)
is.array(Titanic) # TRUE dim(Titanic) # 4 2 2 2 dimnames(Titanic) # lista T <- Titanic dimnames(T) <- list(Clase=c("1ª","2ª","3ª","Tripul."), Sexo=c("Varón","Mujer"), Edad=c("Niño","Adulto"), Sobrevivió=c("No","Sí"))un array es un vector con atributo
dim; otra forma de definir una matriz:> a <- 1:12 > attributes(a) NULL > attr(a,"dim") <- c(3,4) > a [,1] [,2] [,3] [,4] [1,] 1 4 7 10 [2,] 2 5 8 11 [3,] 3 6 9 12
también se puede usar
applycon tensoresh <- HairEyeColor dim(h) # 4 4 2 dimnames(h) apply (h, "Sex", sum) # pueden usarse cadenas en vez de índices apply (h, c("Hair","Eye"), sum) # equivale a: apply (h, 1:2, sum)
- ejercicio
- calcula el porcentaje de supervivientes según la clase en el tensor
Titanic
- calcula el porcentaje de supervivientes según la clase en el tensor
6.3.4 dataframes
se pueden pegar verticalmente con
rbindd <- data.frame (x = 1:5, y = c("uno","dos","tres","cuatro","cinco"), z = 11:15) rbind (d[3:5,], d[1:2,])pero pueden dar problemas si tienen distintas columnas:
(d1 <- d[1:2]) (d2 <- d[2:3]) rbind(d1,d2) # Error in match.names(clabs, names(xi)) : # names do not match previous names mi.rbind <- function (x, y) # para dataframes { nx <- names(x) ny <- names(y) for (nombre in setdiff (nx, ny)) y[[nombre]] <- rep(NA,nrow(y)) for (nombre in setdiff (ny, nx)) x[[nombre]] <- rep(NA,nrow(x)) rbind (x, y) } mi.rbind(d1,d2) ## o recurriendo a biblotecas: dplyr::bind_rows(d1,d2)se pueden cruzar usando
mergeindicando las columnas con identificadoresD <- data.frame(id = c(1,4,5), grupo = c("A","A","B")) merge (d, D, by.x="x", by.y="id") merge (d, D, by.x="x", by.y="id", all=TRUE)esta última versión incluye todos los registros, rellenando con NA en caso necesario
- ejercicios
- combina en un único dataframe los datos
2010..2018/vale002.csvde ./dat/aireUO/dat/csv combina en un único dataframe
pedydatpedydat0
del fichero ./dat/datped.rda
- combina en un único dataframe los datos
6.4 gráficos
6.4.1 plot
- ejemplo
- sea \(X\sim\mathcal B(n=10,p=0.7)\) y sea una muestra
x <- rbinom (100, 10, 0.7) - sea \( Y_i \sim\mathcal P(\lambda=x_i) \) y sea
y <- rpois (100, x)
- sea \(X\sim\mathcal B(n=10,p=0.7)\) y sea una muestra
secuencias
plot (x) plot (x, type = "p") # puntos plot (x, type = "l") # líneas plot (x, type = "b") # ambos (both) plot (x, type = "h") # «histograma»
gráfico de dispersión de
ysobrexplot (x, y) plot (y ~ x) # «fórmula» plot (y ~ x, datos) # si «x» y «y» en dataframe «datos» with (datos, plot (y ~ x)) # idem
gráfico de una función en un intervalo
plot (sin, -pi, pi)
6.4.2 boxplot, hist, barplot, pie
cajas
boxplot(x)
histograma
hist(x)
tallos y hojas
stem(x)
barras y sectores
barplot(table(x)) pie(table(x))
6.4.3 abline, lines, points, text
Para añadir elementos a gráficos ya creados mediante plot, etc.:
recta \(y=a+b\cdot x\)
abline(a,b)
Por ejemplo:
plot (y ~ x) abline (lm (y ~ x), col=2, lwd=3) # col = color; lwd = anchura de la recta
lines (x, y)para añadir líneaspoints (x, y)para añadir puntostext (x, y, etiquetas)para añadir textos
6.4.4 png
Para que los gráficos vayan a un fichero pixelado. Por ejemplo:
png() plot(y~x) plot(x~y) dev.off() # para que cierre correctamente los ficheros .png
6.4.5 pdf
Para que los gráficos vaya a un fichero vectorial.
pdf() # mete todos los gráficos subsiguientes en Rplots.pdf pdf(onefile=FALSE) # crea un .pdf por cada gráfica
Hay que terminar usando dev.off() al igual que con png()
6.4.6 dev.off()
Sirve para que los gráficos se cierren correctamente. Si no se usase, podrían quedar operaciones pendiente y el gráfico podría estar sin terminar.
6.4.7 savePlot
Para guardar un gráfico ya expuesto en una ventana.
savePlot()
6.5 modelos
Consultar el capítulo 11 de Una introducción a R. Por ejemplo:
modelo lineal
y ~ x
modelo cuadrático
y ~ x + I(x^2)
El «+» expresa que se añade un nuevo término al modelo.
Es necesario usar
Icuando el significado de un operador tenga un significado en el lenguaje de modelos distinto del aritmético.resto de variables
y ~ .
Un punto representa al resto de variables que no son la dependiente. Por ejemplo,
lm (mpg ~ . , mtcars)
Son regresores todas las variables salvo
mpg.
6.5.1 regresión simple
- predecir Y a partir de X: \(Y = \beta_0 + \beta_1\,X + \epsilon\)
- los \(\beta\) se estiman a partir de los datos \(x_i,y_i\), \(i=1,...,n\) minimizando los residuos \(e_i\): \[\sum_{i=1}^n e_i^2 = \sum \left(y_i - \beta_0-\beta_1\,x_i \right)^2 \]
- la calidad predictiva suele expresarse mediante el coeficiente de determinación \[ R^2 = \frac {\mbox{variación de Y explicada por el modelo}} {\mbox{variación total de Y}} \]
para construir un modelo, elegir la variable más relacionada con la respuesta
> sort (cor (mtcars) [,1] ^ 2) qsec gear carb am vs drat hp disp 0.1752963 0.2306734 0.3035184 0.3597989 0.4409477 0.4639952 0.6024373 0.7183433 cyl wt mpg 0.7261800 0.7528328 1.0000000 > summary (lm (mpg ~ wt, mtcars)) Call: lm(formula = mpg ~ wt, data = mtcars) Residuals: Min 1Q Median 3Q Max -4.5432 -2.3647 -0.1252 1.4096 6.8727 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 37.2851 1.8776 19.858 < 2e-16 *** wt -5.3445 0.5591 -9.559 1.29e-10 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 3.046 on 30 degrees of freedom Multiple R-squared: 0.7528,Adjusted R-squared: 0.7446 F-statistic: 91.38 on 1 and 30 DF, p-value: 1.294e-10predecir con intervalo de confianza:
> predict (modelo, data.frame (wt = 5), interval="confidence", level=0.99) fit lwr upr 1 10.56277 7.447369 13.67817 > predict (modelo, data.frame (wt = 5), interval="confidence", level=0.95) fit lwr upr 1 10.56277 8.24913 12.87641 > abscisas <- data.frame (wt = seq (min(mtcars$wt), max(mtcars$wt), length.out=100)) > p <- predict (modelo, abscisas, interval="prediction") > head (p) fit lwr upr 1 29.19894 22.58903 35.80885 2 28.98781 22.39104 35.58458 3 28.77667 22.19276 35.36059 4 28.56554 21.99420 35.13688 5 28.35441 21.79535 34.91346 6 28.14327 21.59621 34.69033 > plot (mpg ~ wt, mtcars) > abline (modelo <- lm (mpg ~ wt, mtcars), col = 2) > lines (abscisas$wt, p[,"lwr"], col=3) > lines (abscisas$wt, p[,"upr"], col=3)
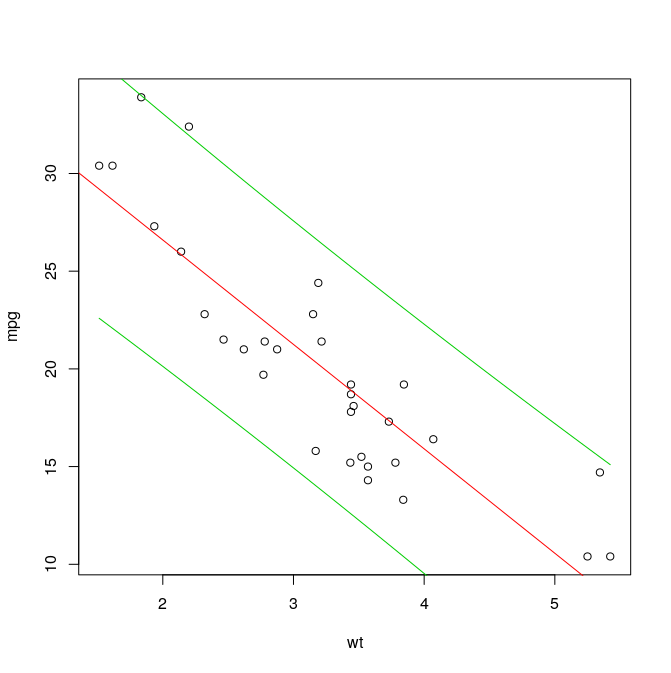
- diagnosis
¿se ajusta la nube de puntos a la recta?: diagrama de dispersión
plot (X, Y)
residuos
plot (lm (Y ~ X))
- deben no presentar estructura
- el gráfico QQ (cuantil - cuantil) muestra su gausianidad
6.5.2 regresión no lineal
trasformación a regresión lineal
plot (1/mpg ~ wt, mtcars) lm (1/mpg ~ wt, mtcars) -> modelo summary (modelo) abline (modelo, col = 2) abscisas <- data.frame (wt = seq (min(mtcars$wt), max(mtcars$wt), length.out=100)) p <- predict (modelo, abscisas, interval="prediction") lines (abscisas$wt, p[,"lwr"], col=3) lines (abscisas$wt, p[,"upr"], col=3)
probar también
mpg ~ log(wt)para expresiones más complejas puede usarse «nls»
> x <- -(1:100)/10 > y <- 100 + 10 * exp(x / 2) + rnorm(x)/10 > nlmod <- nls(y ~ Const + A * exp(B * x)) Warning message: In nls(y ~ Const + A * exp(B * x)) : No starting values specified for some parameters. Initializing ‘Const’, ‘A’, ‘B’ to '1.'. Consider specifying 'start' or using a selfStart model > nlmod Nonlinear regression model model: y ~ Const + A * exp(B * x) data: parent.frame() Const A B 99.9807 10.0175 0.4964 residual sum-of-squares: 0.8255 Number of iterations to convergence: 10 Achieved convergence tolerance: 2.925e-07
6.5.3 regresión múltiple
- lenguaje de modelos de R: capítulo 11 de Una introducción a R
una variable y trasformaciones suyas
> modelo2 <- lm (mpg ~ wt + I(wt^2), mtcars) > summary (modelo2) Call: lm(formula = mpg ~ wt + I(wt^2), data = mtcars) Residuals: Min 1Q Median 3Q Max -3.483 -1.998 -0.773 1.462 6.238 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 49.9308 4.2113 11.856 1.21e-12 *** wt -13.3803 2.5140 -5.322 1.04e-05 *** I(wt^2) 1.1711 0.3594 3.258 0.00286 ** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 2.651 on 29 degrees of freedom Multiple R-squared: 0.8191,Adjusted R-squared: 0.8066 F-statistic: 65.64 on 2 and 29 DF, p-value: 1.715e-11 > abscisas <- data.frame (wt = seq (min(mtcars$wt), max(mtcars$wt), length.out=100)) > p <- predict (modelo2, abscisas, interval="prediction") > plot (mpg ~ wt, mtcars) > lines (abscisas$wt, p[,"fit"], col=2) > lines (abscisas$wt, p[,"lwr"], col=3) > lines (abscisas$wt, p[,"upr"], col=3)
varias variables
> summary (lm (mpg ~ ., mtcars)) # «.» significa «el resto de columnas» Call: lm(formula = mpg ~ ., data = mtcars) Residuals: Min 1Q Median 3Q Max -3.4506 -1.6044 -0.1196 1.2193 4.6271 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 12.30337 18.71788 0.657 0.5181 cyl -0.11144 1.04502 -0.107 0.9161 disp 0.01334 0.01786 0.747 0.4635 hp -0.02148 0.02177 -0.987 0.3350 drat 0.78711 1.63537 0.481 0.6353 wt -3.71530 1.89441 -1.961 0.0633 . qsec 0.82104 0.73084 1.123 0.2739 vs 0.31776 2.10451 0.151 0.8814 am 2.52023 2.05665 1.225 0.2340 gear 0.65541 1.49326 0.439 0.6652 carb -0.19942 0.82875 -0.241 0.8122 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 2.65 on 21 degrees of freedom Multiple R-squared: 0.869,Adjusted R-squared: 0.8066 F-statistic: 13.93 on 10 and 21 DF, p-value: 3.793e-07 > step (lm (mpg ~ ., mtcars)) -> mejor.modelo > summary (mejor.modelo) Call: lm(formula = mpg ~ wt + qsec + am, data = mtcars) Residuals: Min 1Q Median 3Q Max -3.4811 -1.5555 -0.7257 1.4110 4.6610 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 9.6178 6.9596 1.382 0.177915 wt -3.9165 0.7112 -5.507 6.95e-06 *** qsec 1.2259 0.2887 4.247 0.000216 *** am 2.9358 1.4109 2.081 0.046716 * --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 2.459 on 28 degrees of freedom Multiple R-squared: 0.8497,Adjusted R-squared: 0.8336 F-statistic: 52.75 on 3 and 28 DF, p-value: 1.21e-11
- EJERCICIO
- Aplicar «step» al modelo «lm (mpg ~ wt + I(wt2), mtcars)» para obtener un modelo nuevo.
- Comparar gráficamente predicciones e intervalos de ambos modelos.
6.5.4 análisis de varianza de efectos fijos
6.5.4.1 unifactorial
Libro (libre) de inferencia de la Universidad de Cádiz
análisis de varianza unifactorial: «aov (respuesta ~ grupo, …)»
library (car) # para Chile summary (aov (statusquo ~ vote, Chile))
- modelo
- variable respuesta \(X\)
- factor \(A\) con \(I\) niveles indexados por \(i=1,...,I\)
- \(X_i = \mu_i+\epsilon_i = \mu + a_i + \epsilon_i\)
- \(\epsilon_i \hookrightarrow N(0;\sigma)\)
| Nivel | Observaciones | Total | Media muestral | Media poblacional |
|---|---|---|---|---|
| 1 | \(\begin{array}{cccc}x_{11} & x_{12} & \ldots & x_{1n_{1}} \\\end{array}\) | \(x_{1\cdot}\) | \(\bar{x}_1\) | \(\mu_{1}\) |
| 2 | \(\begin{array}{cccc}x_{21}&x_{22}&\ldots &x_{2n_{2}}\\\end{array}\) | \(x_{2\cdot}\) | \(\bar{x}_2\) | \(\mu_{2}\) |
| \(\vdots\) | \(\begin{array}{llcr}\vdots &\vdots & &\vdots \\\end{array}\) | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| I | \(\begin{array}{cccc}x_{I1}&x_{I2}&\ldots &x_{In_{I}}\\\end{array}\) | \(x_{I\cdot}\) | \(\bar{x}_I\) | \(\mu_{I}\) |
| Valores globales | \(x_{\cdot\cdot}\) | \(\bar{x}_{..}\) | \(\mu\) |
- contraste
- \( H_0: \quad \mu_1=\mu_2=...=\mu_I \quad\equiv\quad \forall\,i,\,\mu_i=\mu\quad\equiv\quad \forall\,i,\,a_i=0 \)
- \( H_1: \quad \exists\,i,j,\, \mu_i\not=\mu_j\quad \equiv\quad \exists\,i,\, a_i\not=0\)
- descomposición de la variabilidad \[x_{ij}=\mu+a_{i}+\varepsilon_{ij}\] \[x_{ij}=\bar{x}_{\cdot\cdot}+(\bar{x}_{i\cdot}-\bar{x}_{\cdot\cdot})+(x_{ij}-\bar{x}_{i\cdot})\] \[(x_{ij}-\bar{x}_{\cdot\cdot})=(\bar{x}_{i\cdot}-\bar{x}_{\cdot\cdot})+(x_{ij}-\bar{x}_{i\cdot})\] \[\sum_{i=1}^k\sum_{j=1}^{n_{i}}(x_{ij}-\bar{x}_{\cdot\cdot})^2= \sum_{i=1}^k\sum_{j=1}^{n_{i}}[(\bar{x}_{i\cdot}-\bar{x}_{\cdot\cdot}) +(x_{ij}-\bar{x}_{i\cdot})]^2\] \[\underbrace{\sum_{i=1}^k\sum_{j=1}^{n_{i}}(x_{ij}-\bar{x}_{\cdot\cdot})^2}_{SC{T}}= \underbrace{\sum_{i=1}^k n_{i}(\bar{x}_{i\cdot}-\bar{x}_{\cdot\cdot})^2}_{SC{A}}+ \underbrace{\sum_{i=1}^k\sum_{j=1}^{n_{i}}(x_{ij}-\bar{x}_{i\cdot})^2}_{SC{E}} \]
en R
summary (aov (Speed ~ Expt, morley)) # ¡ojo a los grados de libertad! summary (aov (Speed ~ factor(Expt), morley)) summary (lm (Speed ~ factor(Expt), morley)) # equivalente
6.5.4.2 bifactorial
- modelo
- variable respuesta \(X\)
- factor \(A\) con \(I\) niveles indexados por \(i=1,...,I\)
- factor \(B\) con \(J\) niveles indexados por \(j=1,...,J\)
- \(X_i = \mu + a_i + b_j+\epsilon_{ij}\)
- \(X_i = \mu + a_i + b_j+ (ab)_{ij} + \epsilon_{ij}\) (con interacción)
- \(\epsilon_{ij} \hookrightarrow N(0;\sigma)\)
lenguaje de modelos de R: capítulo 11 de Una introducción a R
summary (sin <- aov (yield ~ N+P, npk)) # sin interacción summary (con <- aov (yield ~ N*P, npk)) # con interacción summary (aov (yield ~ N+P+N:P, npk)) # ídem anova (sin, con) # contraste para comparar
6.5.4.3 multifactorial
puede haber interacciones entre tres o más factores
summary (aov (statusquo ~ region + sex + education, Chile)) summary (lm (statusquo ~ region + sex + education, Chile)) summary (aov (yield ~ N*P*K*block, npk)) # sin grados de libertad suficientes summary (aov (yield ~ N*P*K+block, npk)) # el bloque se supone sin interacción summary (aov (yield ~ N+K+block, npk)) summary (lm (yield ~ N+K+block, npk)) # ver diferencias entre bloques
6.6 generar aleatorios
para muestrear se usa
samplesample (6) # permuta números del 1 al 6 sample (letters) # permuta un vector arbitrario sample (6, 1) # 1 tirada de dado hexagonal sample (letters, 3) # tres letras que no se repiten sample (6, 10, replace=TRUE) # 10 tiradas de dado sample (c("M","H"), 100, replace=TRUE, prob=c(.49,.51)) # no equiprobablespara muestrear de una variable aleatoria, se usan funciones cuyos nombres comienzan por
r:rbinom,rexp,rpois,rnorm,runif…hist (rnorm(10000), breaks=100) hist (runif(10000), breaks=100)
(sustituyendo la
rinicial pordtendríamos la densidad; porp, tendríamos la función de distribución; porq, la función cuantil)
6.7 paquetes
- las definiciones de variables pueden no estar disponibles en la instalación básica de R, pero sí en bibliotecas o paquetes
para ver qué paquetes están instalados:
installed.packages ()
para usar una función definida en un paquete:
e1071::skewness (rexp (10))
o bien
library (e1071) # o library("e1071") skewness (rexp (10))para instalar un paquete no instalado:
install.packages ("primes") primes::is_prime (101) # sólo funciona si "primes" está instaladopara actualizar todos los paquetes instalados:
update.packages (ask = FALSE)
6.8 medir tiempos de ejecución
En general, nos interesará el indicado como «elapsed».
6.8.1 system.time
Se encierran las instrucciones dentro de una llamada a system.time:
> system.time ({Sys.sleep(5); Sys.sleep(5)})
user system elapsed
0.00 0.00 10.01
6.8.2 proc.time
Se llama a proc.time antes y después de la ejecución, y se restan los valores:
comienzo <- proc.time () Sys.sleep(5) Sys.sleep(5) final <- proc.time () final - comienzo
6.9 manejo de errores, avisos y datos ausentes
6.9.1 try
Sobre todo a la hora de realizar bucles,
podemos encontrar molesto que la ocurrencia de un error en una iteración
implique la pérdida de los cálculos de las demás iteraciones.
Para evitarlo se puede usar try :
sapply (c(3,2,1,0,1,2), function(x) if (x) 10*x else no.existo) sapply (c(3,2,1,0,1,2), function(x) try (if (x) 10*x else no.existo))
Para aprovechar los resultados, puede ser necesario usar «as.numeric»:
as.numeric (sapply (c(3,2,1,0,1,2), function(x) try (if (x) 10*x else no.existo)))
o usar inherits(...,"try-error") como se explica en la ayuda de try
Filter (function (x) !inherits(x,"try-error"), lapply (c(3,2,1,0,1,2), function(x) try (if (x) 1:x else no.existo, silent = TRUE)))
6.9.2 depurar mediante browser
Si en la definición de una función incluimos una llamada a browser(),
entramos en el depurador y podemos:
- evaluar expresiones, incluyendo variables locales
- ejecutar paso a paso con la orden
n(next) - continuar con la ejecución mediante
c - interrumpir la ejecución mediante
Q(quit)
He aquí un ejemplo de sesión, en la que se define una función para calcular el coefciente de variación:
> coef.var <- function (x) {media <- mean(x); dt <- sd(x); dt/media} > muestra <- c(0, -9, 5, 0, 4) > coef.var (muestra) [1] Inf > coef.var <- function (x) {browser(); media <- mean(x); dt <- sd(x); dt/media} > coef.var (muestra) Called from: coef.var(muestra) Browse[1]> debug en #1: media <- mean(x) Browse[2]> n debug en #1: dt <- sd(x) Browse[2]> media [1] 0 Browse[2]> n debug en #1: dt/media Browse[2]> dt [1] 5.522681 Browse[2]> c [1] Inf >
Hemos explorado qué valores toman dt y media dentro de la función,
de forma que comprobamos in situ que se realiza una división por cero.
6.9.3 suppressWarnings
Si queremos evitar avisos que prevemos, podemos usar suppressWarnings :
edad <- c("15", "62", "no desvela su edad", "48", "no contesta") as.numeric (edad) suppressWarnings (as.numeric (edad))
Puede interesar también la opción «silent=TRUE» de try.
6.9.4 na.action
Para usar ciertas funciones es aconsejable cambiar el comportamiento habitual de R con los NA (datos ausentes). Por ejemplo, podemos tener interés en incorporar a los datos originales las puntuaciones (scores) resultantes de un anásisis de componentes principales:
options ("na.action") # na.omit por omisión ## ejemplo de ?na.omit ?na.exclude DF <- data.frame(x = c(1, 2, 3), y = c(0, 10, NA)) na.omit(DF) p <- princomp (~ x + y, DF) # análisis de componentes principales p$scores # sólo para dos individuos options (na.action = na.exclude) p <- princomp (~ x + y, DF) # ACP, lo mismo que antes p$scores # también para el tercero (aunque tenga NA) DF$acp1 <- p$scores[,1] # lo que permite pegarlo al dataframe original
La interfaz Rcmdr efectúa esa acción de forma predeterminada.
La asignación de opciones puede hacerse de varias formas:
options (na.action = na.exclude) # se asigna una función options (na.action = "na.exclude") # se asigna una cadena con el nombre de la función options ("na.action" = na.exclude) # el nombre de la opción puede estar entrecomillado options ("na.action" = "na.exclude")
El resultado de cada asignación puede comprobarse con
options ("na.action") options()$na.action # mismo efecto
pero
options (na.action)
da error, porque los argumentos de "options" han de ser cadenas (con el nombre de las opciones) o parejas de la forma: etiqueta = valor.
6.10 expresiones regulares (regexp)
Para manejar cadenas de texto.
Las expresiones regulares interpretan algunos caracteres de forma especial.
- «
.» corresponde a cualquier carácter - «
^» corresponde a inicio de cadena - «
$» corresponde a fin de cadena - «
*» cero o más presencias de lo precedente - «
+» una o más presencias de lo precedente - «
|» o bien lo de la izquierda o bien lo de la derecha - «
[...]» grupo de caracteres; por ejemplo[aeiou]representa una vocal minúscula - «
[...-...]» rango de caracteres; por ejemplo[0-9]representa un dígito - «
\» quita el comportamiento especial a un carácter (ha de usarse doble dentro de una cadena de R) - «
\w» corresponde a un signo alfanumérico - «
\d» corresponde a un dígito decimal - «
cosa» corresponde a la cadena «cosa»
Hay más información en la ayuda «?regex» de R y en la wikipedia.
6.10.1 coincidencia exacta
v <- c("Villa","Luanco","Villaviciosa","Candás","Pendones","Villa","Veranes") which (v=="Villa") # devuelve posiciones de todos match ("Villa", v) # devuelve posición del primero grep ("^Villa$", v) # devuelve posiciones de todos grep ("^Villa$", v, value=TRUE) # devuelve todas las cadenas congruentes
6.10.2 coincidencia con una parte
grep ("Villa", v) # posiciones de cada cadena que contiene Villa grep ("Villa", v, value=TRUE) # devuelve valores grep ("c", v, ignore.case=TRUE) # contienen «c» mayúscula o minúscula grep ("^V", v) # empiezan por «V» grep ("s$", v) # terminan por «s»
6.10.3 coincidencia con patrones más genéricos
grep ("[aeiou]", letters) # las vocales grep ("[^aeiou]", letters) # las consonantes (el circunflejo niega) grep ("[a-dx-z]", letters) # las cuatro primeras letras o las tres últimas grep ("^V.*a$", v) # empieza por «V» y acaba en «a» ficheros <- system ("ls -a ~", intern=TRUE) # todos los de la carpeta personal grep ("^\\.", ficheros, value=TRUE) # ficheros ocultos; empiezan por .
En este último caso,
grep ("^.", ...)no funcionaría porque.se refiere a cualquier caráctergrep ("^.", ..., fixed=TRUE)no funcionaría porquefixed=TRUEimpediría el significado especial de^grep (".", ..., fixed=TRUE)no funcionaría porque incluiría ficheros no ocultos cuyo nombre contiene un puntogrep ("^\.", ...)no funcionaría porque\es el «carácter de escape» de las cadenas de R, y\.no es una secuencia de escape reconocidagrep ("^\\.", ...)funciona porque la cadena^\\.es la representación externa en R de la cadena interna^\.:> nchar ("^\\.") [1] 3 > substr ("^\\.", 1,1) [1] "^" > substr ("^\\.", 2,2) [1] "\\" > substr ("^\\.", 3,3) [1] "."
6.11 funciones genéricas (orientación a objetos)
- la instalación básica de R contiene dos sistemas de objetos
- el llamado S3, que comentaremos en esta sección
- el llamado S4, un sistema más formal pero no tan extendido como S3; no lo detallaremos
- características de un sistema orientado a objetos
polimorfismo: una función se comporta de manera distinta en función de su argumento
summary (mtcars $ am) # el argumento es un vector numérico => media y 5 cuartiles summary (factor (mtcars $ am)) # el argumento es un factor => tabla de frecuencias absolutas
clase: el tipo de objeto
class (mtcars $ am) # el argumento es un vector numérico class (factor (mtcars $ am)) # el argumento es un factor
- función genérica: una función que acepta argumentos de distintas clases
y se comporta de forma distinta según la clase; por ejemplo,
summary método: implementación de una función genérica para cierta clase de argumentos
methods (summary) # qué metodos hay definidos para "summary" summary.factor # implementación para factores summary.default # implementación por omisión, p.ej. para vectores numéricos summary.lm # implementación para modelos lineales summary.ecdf # error porque está indicado con * al ejecutar "methods(summary)" getAnywhere (summary.ecdf) # forzamos la obtención del código fuente de dicho método
- objetos S3 en R
para estudiar el tipo de un objeto, se usan
classymodem <- matrix (1:12, 3) class (m) # matrix mode (m) # integer class (mtcars) # data.frame mode (mtcars) # list class (1:5) # integer class (sum) # function class (function (x) x^2) # function class (by(mtcars$mpg,mtcars$am,mean) # by
a un objeto de R se le pueden asociar atributos
ob <- 1:5 attributes(ob) # NULL attr(ob,"creador") <- "carlos" ob attributes(ob) attributes(ob)$creador 100 * ob # el objeto sigue comportándose normalmente
si un objeto tiene un atributo llamado
classentonces ése determina su claseefe <- factor (c ("a", "a", "b")) efe attributes (efe) # levels y class unclass (efe) # un vector numérico
a veces puede interesar deshacerse de la clase
resumen <- with (mtcars, by (wt, list(AM=am,VS=vs), median)) resumenA <- unclass (resumen) # conseguimos una matriz attr(resumenA,"call") <- NULL # eliminamos atributos sobrantes
podemos inventar nuevas clases y definir métodos para ellas
efe <- rbinom (10, 5, 0.3) class(efe) <- "cuandiscreta" # cuantitativa discreta attributes(efe) # class print.cuandiscreta <- function (x) print (factor (x)) # se muestran los niveles... efe # aplica el me'todo "print" efe * 100 # pero puede usarse numéricamente summary.cuandiscreta <- function (x) { cat ("Cuantitativamente:\n") print (summary (as.numeric (x))) cat ("Discretamente:\n") print (summary (factor (x))) } summary (efe) # me'todo "summary"
- ejercicios
- modificar el método
summarydecuandiscretapara que dé también porcentajes - crear un método de la función
plotque sea adecuado paracuandiscreta
- modificar el método
6.12 http
obtener una página de internet; varias opciones
library(rvest) ## "top airing anime" de MyAnimeList.net tan <- read_html("https://myanimelist.net/topanime.php?type=airing")
- procesarla; varios enfoques:
recoger todo el texto y tratarlo con funciones de cadena
texto <- html_text(tan) # también vale html_text2 inicio <- regexpr("Shingeki",texto) registros <- strsplit(substring(texto, inicio), "Add to list")[[1]] campos <- strsplit(registros, "\n") campos <- lapply(campos, trimws) # quita blancos extremos de cada campo no.vacia <- function (x) nchar(x) > 0 # para cadenas campos <- lapply(campos, function (x) Filter(no.vacia, x)) ## primer campo = posición (salvo en el primero) ## segundo campo = título ## penúltimo campo = puntaje campos[[1]] <- c("1", campos[[1]]) # añade posición al primero tabla <- t (sapply (campos, function (x) x[c(1,2,length(x)-1)])) tabla <- tabla[1:50,] # el 51 indica un enlace a más datos tabla <- data.frame(tabla, stringsAsFactors=TRUE) names(tabla) <- c("pos", "titulo","puntaje") tabla$puntaje <- as.numeric(as.character(tabla$puntaje))
buscar nodo concreto (de tipo "table")
tabla <- html_table(html_element(tan,"table")) names(tabla) <- unlist(tabla[1,]) tabla <- tabla[-1,c("Title","Score")] tabla$Title <- sapply(strsplit(tabla$Title,"\n"),function(x)x[1]) tabla$Score <- as.numeric(tabla$Score)
usar la estructura de HTMl como XML como lista de R
library(XML) fichero <- tempfile() download.file("https://myanimelist.net/topanime.php?type=airing",fichero) arbol <- htmlTreeParse(fichero) arbol <- xmlToList (arbol$children$html)